题目内容
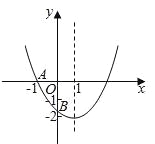
【题目】如图,已知二次函数y=ax2+bx+c(a≠0)的图象与x轴交于点A(﹣1,0),与y轴的交点B在(0,﹣2)和(0,﹣1)之间(不包括这两点),对称轴为直线x=1.下列结论:①abc>0 ②4a+2b+c>0 ③4ac﹣b2<8a ④![]() <a<
<a<![]() ⑤b>c.其中含所有正确结论的选项是( )
⑤b>c.其中含所有正确结论的选项是( )
A.①③ B.①③④ C.②④⑤ D.①③④⑤
【答案】D
【解析】
试题分析:根据对称轴为直线x=1及图象开口向下可判断出a、b、c的符号,从而判断①;根据对称轴得到函数图象经过(3,0),则得②的判断;根据图象经过(﹣1,0)可得到a、b、c之间的关系,从而对②⑤作判断;从图象与y轴的交点B在(0,﹣2)和(0,﹣1)之间可以判断c的大小得出④的正误.
①∵函数开口方向向上, ∴a>0; ∵对称轴在y轴右侧 ∴ab异号,
∵抛物线与y轴交点在y轴负半轴, ∴c<0, ∴abc>0, 故①正确;
②∵图象与x轴交于点A(﹣1,0),对称轴为直线x=1, ∴图象与x轴的另一个交点为(3,0),
∴当x=2时,y<0, ∴4a+2b+c<0, 故②错误; ③∵图象与x轴交于点A(﹣1,0),
∴当x=﹣1时,y=(﹣1)2a+b×(﹣1)+c=0, ∴a﹣b+c=0,即a=b﹣c,c=b﹣a,
∵对称轴为直线x=1 ∴-![]() =1,即b=﹣2a, ∴c=b﹣a=(﹣2a)﹣a=﹣3a,
=1,即b=﹣2a, ∴c=b﹣a=(﹣2a)﹣a=﹣3a,
∴4ac﹣b2=4a(﹣3a)﹣(﹣2a)2=﹣16a2<0 ∵8a>0 ∴4ac﹣b2<8a 故③正确
④∵图象与y轴的交点B在(0,﹣2)和(0,﹣1)之间, ∴﹣2<c<﹣1 ∴﹣2<﹣3a<﹣1,
∴![]() >a>
>a>![]() ; 故④正确 ⑤∵a>0, ∴b﹣c>0,即b>c; 故⑤正确;
; 故④正确 ⑤∵a>0, ∴b﹣c>0,即b>c; 故⑤正确;

练习册系列答案
 轻松课堂单元测试AB卷系列答案
轻松课堂单元测试AB卷系列答案 小题狂做系列答案
小题狂做系列答案
相关题目
