题目内容
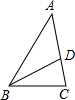 填写下列解题过程中的推理根据:
填写下列解题过程中的推理根据:
如图,在△ABC中,∠A=40°,∠ABC的平分线BD交AC于点D,∠BDC=70°,求∠C的度数.
对于上述问题,在以下解答过程的空白处填上适当的内容(理由或数学式)
解:∵∠BDC=∠A+∠ABD
(________)
∵∠A=40°,∠BDC=70°(已知)
∴∠ABD=________°(等式的性质)
∵BD平分∠ABC(已知)
∴∠ABC=2∠ABD(________)
∴∠ABC=60°(等式的性质)
∵∠A+∠ABC+∠C=________°(三角形的内角和是180°)
∠A=40°(已知),∠ABC=60°(已求)
∴∠C=________°(等式的性质)
三角形的一个外角等于与它不相邻的两个内角的和 30 角平分线的定义 180 80
分析:首先能够准确叙述定理,根据所给的证明过程说明理由.
解答:∵∠BDC=∠A+∠ABD
(三角形的一个外角等于与它不相邻的两个内角的和)
∵∠A=40°,∠BDC=70°(已知)
∴∠ABD=30°(等式的性质)
∵BD平分∠ABC(已知)
∴∠ABC=2∠ABD(角平分线的定义)
∴∠ABC=60°(等式的性质)
∵∠A+∠ABC+∠C=180°(三角形的内角和是180°)
∠A=40°(已知),∠ABC=60°(已求)
∴∠C=80°(等式的性质).
点评:考查了三角形的内角和定理及其推论,理解角平分线的概念.
分析:首先能够准确叙述定理,根据所给的证明过程说明理由.
解答:∵∠BDC=∠A+∠ABD
(三角形的一个外角等于与它不相邻的两个内角的和)
∵∠A=40°,∠BDC=70°(已知)
∴∠ABD=30°(等式的性质)
∵BD平分∠ABC(已知)
∴∠ABC=2∠ABD(角平分线的定义)
∴∠ABC=60°(等式的性质)
∵∠A+∠ABC+∠C=180°(三角形的内角和是180°)
∠A=40°(已知),∠ABC=60°(已求)
∴∠C=80°(等式的性质).
点评:考查了三角形的内角和定理及其推论,理解角平分线的概念.

练习册系列答案
相关题目
 25、填写下列解题过程中的推理根据:
25、填写下列解题过程中的推理根据:


