题目内容
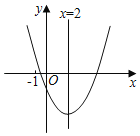
【题目】如图,已知二次函数y=ax2+bx+c(a≠0)的图象如图所示,有下列5个结论:①abc<0;②b<a+c;③4a+2b+c>0;④2c<3b;⑤a+b<m (am+b)(m≠1的实数).其中正确结论的有( )
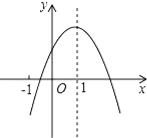
A. ①②③ B. ①③④ C. ③④⑤ D. ②③⑤
【答案】B
【解析】试题分析:①图象开口向下,与y轴交于正半轴,对称轴为x=1,能得到:a<0,c>0,-![]() =1,
=1,
∴b=-2a>0,
∴abc<0,
所以①正确;
②当x=-1时,由图象知y<0,
把x=-1代入解析式得:a-b+c<0,
∴b>a+c,
∴②错误;
③图象开口向下,与y轴交于正半轴,对称轴为x=1,
能得到:a<0,c>0,-![]() =1,
=1,
所以b=-2a,
所以4a+2b+c=4a-4a+c>0.
∴③正确;
④∵由①②知b=-2a且b>a+c,
∴2c<3b,④正确;
⑤图象开口向下,与y轴交于正半轴,对称轴为x=1,能得到:a<0,c>0,-![]() =1,
=1,
∴b=-2a,
∴a+b=a-2a=-a,m(ma+b)=m(m-2)a,
假设a+b<m(am+b),(m≠1的实数)
即-a<m(m-2)a,
所以(m-1)2<0,
不满足题意,所以假设不成立,
∴⑤不正确.
故正确结论是①、③,④.
故选:B.

练习册系列答案
 教育世家状元卷系列答案
教育世家状元卷系列答案 黄冈课堂作业本系列答案
黄冈课堂作业本系列答案 单元加期末复习先锋大考卷系列答案
单元加期末复习先锋大考卷系列答案
相关题目