Question

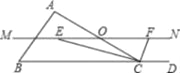
【题目】如图,在△ABC中,点O是AC边上的一点.过点O作直线MN∥BC,设MN交∠BCA的平分线于点E,交∠BCA的外角平分线于F．

（1）求证：EO=FO；（2）若CE=4,CF=3,你还能得到那些结论？

Answer 1

【答案】（1）证明见解析；（2）OE=OF=OC=0.5EF=2.5．

【解析】

（1）利用角平分线加平行线得等腰三角形即可解题；（2）利用角平分线证明∠ECF=90°，勾股定理即可求出斜边的长.

解：（1）如下图,

∵CE是∠ACB的平分线，

∴∠1=∠2，

∵MN∥BC，

∴∠1=∠3，

∴∠2=∠3，

∴OE=OC，同理可得OF=OC，

∴OE=OF；

（2）∵CE是∠ACB的平分线，

∴∠1=∠2，

∵CF是∠OCD的平分线，

∴∠4=∠5，

∴∠ECF=90°，

在Rt△ECF中，由勾股定理得EF=．

∴OE=OF=OC=EF=2.5．