题目内容
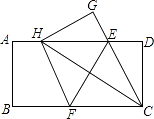
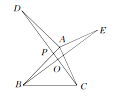
【题目】如图所示,DA⊥AB,EA⊥AC,AB=AD,AC=AE,BE和CD相交于O,AB和CD相交于P,则∠DOE的度数是____.
【答案】90°
【解析】
根据已知条件易证得△AEB≌△ACD,可得∠D=∠ABE,由DA⊥AB可得∠D+∠APD=90°,而由图可知∠APD和∠BPO是对顶角相等,即可得∠DOE=∠DOB=90°.
解:∵DA⊥AB,EA⊥AC,
∴∠DAB=∠CAE=90°,
∴∠DAB+∠BAC=∠CAE+∠BAC,即∠DAC=∠BAE,
又∵AB=AD,AC=AE,
∴△AEB≌△ACD(SAS),
∴∠D=∠ABE;
∵DA⊥AB,
∴∠D+∠APD=90°,
∵∠APD=∠BPO(对顶角相等),已证得∠D=∠ABE;
∴∠BPO+∠ABE=90°,
∴∠DOE=∠DOB=90°.
故答案为:90°.

练习册系列答案
 应用题天天练四川大学出版社系列答案
应用题天天练四川大学出版社系列答案
相关题目
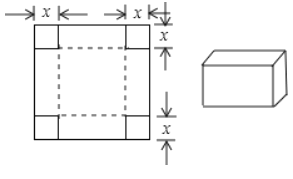
【题目】如图所示,一张边长为![]() 的正方形硬纸板,把它的四个角都剪去一个边长为工
的正方形硬纸板,把它的四个角都剪去一个边长为工![]() (
(![]() 为正整数)的小正方形,然后把它折成一个无盖的长方体,设长方体的容积为
为正整数)的小正方形,然后把它折成一个无盖的长方体,设长方体的容积为![]() ,请回答下列问题:
,请回答下列问题:
(1)用含有![]() 的代数式表示
的代数式表示![]() ,则
,则![]()
(2)完成下表:
| 1 | 2 | 3 | 4 | 5 | 6 | 7 |
|
(3)观察上表,当![]() 取什么值时,容积
取什么值时,容积![]() 的值最大?
的值最大?