题目内容
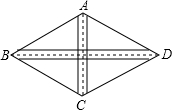
如图，在菱形ABCD中，AE⊥BC于E，EC=1，sinB=
，则四边形AECD的周长=______．
| 5 |
| 13 |
∵sinB=
，AE⊥BC，
∴设AE=5x，AB=13x，
在Rt△ABE中，BE=
=
=12x，
在菱形ABCD中，AB=BC，
∴13x=12x+1，
解得x=1，
∴AE=5，菱形的边长=13，
∴四边形AECD的周长=5+1+13+13=32．
故答案为：32．
| 5 |
| 13 |
∴设AE=5x，AB=13x，
在Rt△ABE中，BE=
| AB2-AE2 |
| (13x)2-(5x)2 |
在菱形ABCD中，AB=BC，
∴13x=12x+1，
解得x=1，
∴AE=5，菱形的边长=13，
∴四边形AECD的周长=5+1+13+13=32．
故答案为：32．
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
