��Ŀ����
 ��ͼ������ABCD�У�AB=6cm��BC=12cm����P��A��ʼ��AB�����B��1����/����ٶ��ƶ�����Q�ӵ�B��ʼ��BC�����C��2����/����ٶ��ƶ�������P����B����Q����C��ʱ������ֹͣ�ƶ������P��Q�ֱ��Ǵ�A��Bͬʱ������t���Ӻ�
��ͼ������ABCD�У�AB=6cm��BC=12cm����P��A��ʼ��AB�����B��1����/����ٶ��ƶ�����Q�ӵ�B��ʼ��BC�����C��2����/����ٶ��ƶ�������P����B����Q����C��ʱ������ֹͣ�ƶ������P��Q�ֱ��Ǵ�A��Bͬʱ������t���Ӻ���1�������PBQ�������
��2������PBQ���������8ƽ������ʱ����t��ֵ��
��3���Ƿ���ڡ�PBQ���������10ƽ�����ף������ڣ����t��ֵ���������ڣ�˵�����ɣ�
��������1����PBQ�����Ϊ
��BP��BQ������BP=AB-AP=6-t��BQ=2t���ֱ��ù���t�Ĵ���ʽ���������ʽ���ɣ�
��2�����ɣ�1������������ʽ�Ĵ���ʽ=8����÷��̵ó�t��ֵ��
��3���������ʹ��PBQ���������10ƽ�����ף��1���Ĵ���ʽ=10�����÷����Ƿ��и���������֤�����ڣ��������ڣ�
| 1 |
| 2 |
��2�����ɣ�1������������ʽ�Ĵ���ʽ=8����÷��̵ó�t��ֵ��
��3���������ʹ��PBQ���������10ƽ�����ף��1���Ĵ���ʽ=10�����÷����Ƿ��и���������֤�����ڣ��������ڣ�
����⣺��1�������⣺AP=t��BQ=2t��BP=6-t
���ԡ�PBQ�����Ϊ��
BP��BQ=
(6-t)2t=-t2+6t��
��2�������⣺-t2+6t=8����t2-6t+8=0
��֮�ã�t1=2��t2=4��
����PBQ���������8ƽ������ʱ��t��ֵΪ2��4��
��3�������ڣ�
������ڡ�PBQ���������10ƽ�����ף�
��-t2+6t=10����t2-6t+10=0����=��-6��2-4��10=-4��0���ʷ�����ʵ������
����ڡ�PBQ���������10ƽ�����ף�
���ԡ�PBQ�����Ϊ��
| 1 |
| 2 |
| 1 |
| 2 |
��2�������⣺-t2+6t=8����t2-6t+8=0
��֮�ã�t1=2��t2=4��
����PBQ���������8ƽ������ʱ��t��ֵΪ2��4��
��3�������ڣ�
������ڡ�PBQ���������10ƽ�����ף�
��-t2+6t=10����t2-6t+10=0����=��-6��2-4��10=-4��0���ʷ�����ʵ������
����ڡ�PBQ���������10ƽ�����ף�
������������Ҫ�������һԪ���η��̵�Ӧ�ã��г���������������Ĺ�ϵʽ���������Ϊ8ƽ����10ƽ����ʱ���г�������⣮

��ϰ��ϵ�д�
 ��У����ϵ�д�
��У����ϵ�д�
�����Ŀ
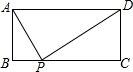 ��ͼ������ABCD�У�AD=a��AB=b��ҪʹBC�������ٴ���һ��P��ʹ��ABP����APD����CDP�������ƣ���a��b��Ĺ�ϵʽһ�����㣨������
��ͼ������ABCD�У�AD=a��AB=b��ҪʹBC�������ٴ���һ��P��ʹ��ABP����APD����CDP�������ƣ���a��b��Ĺ�ϵʽһ�����㣨������A��a��
| ||
| B��a��b | ||
C��a��
| ||
| D��a��2b |
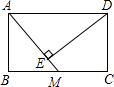 ��ͼ������ABCD�У�AB=6��BC=8��M��BC���е㣬DE��AM��E�Ǵ��㣬���ABM�����Ϊ
��ͼ������ABCD�У�AB=6��BC=8��M��BC���е㣬DE��AM��E�Ǵ��㣬���ABM�����Ϊ 7����ͼ������ABCD�У�AE��BD������ΪE����DAE=2��BAE�����CAE=
7����ͼ������ABCD�У�AE��BD������ΪE����DAE=2��BAE�����CAE= ��2008•��������ģ����֪��ͼ������ABCD�У�AB=3cm��BC=4cm��E�DZ�AD��һ�㣬��BE=ED��P�ǶԽ���������һ�㣬PF��BE��PG��AD������ֱ�ΪF��G����PF+PG�ij�Ϊ
��2008•��������ģ����֪��ͼ������ABCD�У�AB=3cm��BC=4cm��E�DZ�AD��һ�㣬��BE=ED��P�ǶԽ���������һ�㣬PF��BE��PG��AD������ֱ�ΪF��G����PF+PG�ij�Ϊ ��2002•���أ���֪����ͼ������ABCD�У�E��F��AB�������㣬��AF=BE������DE��CF�õ�����EFCD��
��2002•���أ���֪����ͼ������ABCD�У�E��F��AB�������㣬��AF=BE������DE��CF�õ�����EFCD��