Question

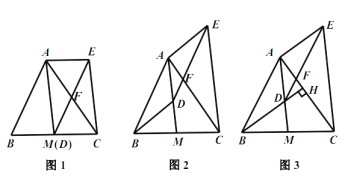
【题目】以△ABC的三边在BC同侧分别作三个等边三角形△ABD，△BCE ，△ACF，试回答下列问题：

（1）四边形ADEF是什么四边形？请证明：

（2）当△ABC满足什么条件时，四边形ADEF是矩形？

（3）当△ABC满足什么条件时，四边形ADEF是菱形？

（4）当△ABC满足什么条件时，能否构成正方形？

（5）当△ABC满足什么条件时，无法构成四边形？

Answer 1

【答案】（1）见解析；（2）当△ABC中的∠BAC=150°时，四边形ADEF是矩形；（3）当△ABC中的AB=AC时，四边形ADEF是菱形；（4）当∠BAC=150°且AB=AC时，四边形ADEF是正方形；（5）当∠BAC=60°时，D、A、F为同一直线，与E点构不成四边形，即以A、D、E、F为顶点的四边形不存在．

【解析】

（1）通过证明△DBE≌△ABC，得到DE=AC，利用等边三角形ACF，可得DE=AF，

同理证明与全等，利用等边三角形，得AD=EF，可得答案．（2）利用平行四边形ADEF是矩形，结合已知条件等边三角形得到即可．（3）利用平行四边形ADEF是菱形形，结合已知条件等边三角形得到即可．（4）结合（2）（3）问可得答案．（5）当四边形ADEF不存在时，即出现三个顶点在一条直线上，因此可得答案。

解：（1） ∵△BCE、△ABD是等边三角形，

∴∠DBA=∠EBC=60°，AB=BD，BE=BC，

∴∠DBE=∠ABC，

∴△DBE≌△ABC，

∴DE=AC，

又△ACF是等边三角形， ∴AC=AF，

∴DE=AF，

同理可证：AD=EF，

∴四边形ADEF是平行四边形．

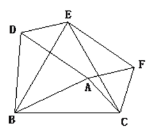
（2） 假设四边形ADEF是矩形， 则∠DAF=90°，

又∠DAB=∠FAC=60°， ∠DAB+∠FAC+∠DAF+∠BAC=360°

∴∠BAC=150°．

因此当△ABC中的∠BAC=150°时，四边形ADEF是矩形．

（3）假设四边形ADEF是菱形， 则AD=DE=EF=AF

∵AB=AD，AC=AF，∴AB=AC

因此当△ABC中的AB=AC时，四边形ADEF是菱形．

（4）结合（2）（3）问可知当∠BAC=150°且AB=AC时，

四边形ADEF是正方形．

（5）由图知道：∠DAB+∠FAC+∠DAF+∠BAC=360°

∴当∠BAC=60°时，D、A、F为同一直线，与E点构不成四边形，

即以A、D、E、F为顶点的四边形不存在．