题目内容
(8分)如图,AB是半圆的直径,点O是圆心,点C是OA的中点,CD⊥OA交
半圆于点D,点E是的中点,连接AE、OD,过点D作DP∥AE交BA的延长线于点P.
(1)求∠AOD的度数;
(2)求证:PD是半圆O的切线.
半圆于点D,点E是的中点,连接AE、OD,过点D作DP∥AE交BA的延长线于点P.
(1)求∠AOD的度数;
(2)求证:PD是半圆O的切线.

(1)解:∵点C时OA的中点,∴OC= OA=
OA= OD
OD
∵CD⊥OA,∴∠OCD=90°。
在Rt△OCD中,cos∠COD=
∴∠COD=60°,即∠AOD=60°。
(2)证明:连结OE,∵点E是 的中点
的中点 ,
,

∴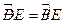 ,
,
∴∠BOE=∠DOE= ∠DOB=
∠DOB= (180°-∠COD)=
(180°-∠COD)= (180°-60°)=60°。
(180°-60°)=60°。
∵OA=OE,∴∠EAO=∠AEO,又∠EAO+∠AEO=∠EOB=60°
∴∠EAO=30°,
∴PD∥AE,
∴∠P=∠EAO=30°。
由(1)知∠AOD=60°,∴∠PDO=180°-(∠P+∠POD)=180°-(30°+60°)=90°,
∴PD是半圆O的切线。
 OA=
OA= OD
OD∵CD⊥OA,∴∠OCD=90°。
在Rt△OCD中,cos∠COD=

∴∠COD=60°,即∠AOD=60°。
(2)证明:连结OE,∵点E是
 的中点
的中点 ,
,
∴
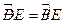 ,
,∴∠BOE=∠DOE=
 ∠DOB=
∠DOB= (180°-∠COD)=
(180°-∠COD)= (180°-60°)=60°。
(180°-60°)=60°。∵OA=OE,∴∠EAO=∠AEO,又∠EAO+∠AEO=∠EOB=60°
∴∠EAO=30°,
∴PD∥AE,
∴∠P=∠EAO=30°。
由(1)知∠AOD=60°,∴∠PDO=180°-(∠P+∠POD)=180°-(30°+60°)=90°,
∴PD是半圆O的切线。
略

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
 和
和 的半径分别是5和4,
的半径分别是5和4,
 ,则
,则 得到△AED,AE交半圆于点F,连接DF。
得到△AED,AE交半圆于点F,连接DF。
 果⊙O的半径是6cm,EC=8cm,求GF的长.
果⊙O的半径是6cm,EC=8cm,求GF的长.
 D是AB 边上的一点,以BD为直径的⊙0与边 AC 相切于点E,连结DE并延长,与BC的延长线交于点 F .
D是AB 边上的一点,以BD为直径的⊙0与边 AC 相切于点E,连结DE并延长,与BC的延长线交于点 F . 
 B.
B. -4
-4
 中,以点(-3,4)为圆心,4为半径的圆
中,以点(-3,4)为圆心,4为半径的圆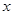 轴相交,与
轴相交,与 轴相切
轴相切