题目内容
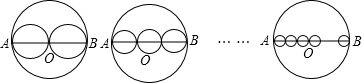
AB是⊙O的直径,把AB分成n条线段,以每条线段为直径分别画小圆,设⊙O的半径为r,那么⊙O的周长l=2πr,⊙O的面积S=πr2.计算:

(1)如图①,把AB分成两条相等的线段,则每个小圆的周长l2=πr=
l;
(2)如图②,把AB分成三条相等的线段,则每个小圆的周长l3=
l
l;
(3)如图③,把AB分成n条相等的线段,则每个小圆的周长ln=
l
l.
(4)如图④,把AB分成n条不相等的线段,记n个小圆的周长分别为Cl,C2,…,Cn,则n个小圆的周长与大圆的周长的关系为
请依照上面的探索方法和步骤,分别计算出如图①、②、③中每个小圆面积与大圆面积的关系.(直接写出结论,不要求写过程)

(1)如图①,把AB分成两条相等的线段,则每个小圆的周长l2=πr=
| 1 |
| 2 |
(2)如图②,把AB分成三条相等的线段,则每个小圆的周长l3=
| 1 |
| 3 |
| 1 |
| 3 |
(3)如图③,把AB分成n条相等的线段,则每个小圆的周长ln=
| 1 |
| n |
| 1 |
| n |
(4)如图④,把AB分成n条不相等的线段,记n个小圆的周长分别为Cl,C2,…,Cn,则n个小圆的周长与大圆的周长的关系为
相等
相等
.请依照上面的探索方法和步骤,分别计算出如图①、②、③中每个小圆面积与大圆面积的关系.(直接写出结论,不要求写过程)
分析:(2)根据圆的半径的变原来的
得出周长即可;
(3)根据圆的半径的变为原来的
得出周长即可;
(4)利用圆的周长公式得出n个小圆的周长与大圆的周长的关系,根据圆的面积公式,将每个圆的面积计算出来即可.
| 1 |
| 3 |
(3)根据圆的半径的变为原来的
| 1 |
| n |
(4)利用圆的周长公式得出n个小圆的周长与大圆的周长的关系,根据圆的面积公式,将每个圆的面积计算出来即可.
解答:解:(2)根据l=2πr,
把AB分成三条相等的线段,每个小圆的周长L3=
×2πr=
l,
故答案为:
l;
(3)把AB分成n条相等的线段,每个小圆的周长Ln=
×2πr=
l.
故答案为:
l;
(4)把AB分成n条不相等的线段,记n个小圆的周长分别为Cl,C2,…,Cn,
则n个小圆的周长为:2π(r1+r2+…+rn)=2πr,
大圆的周长的关系为:2πr,
故n个小圆的周长与大圆的周长的关系为:相等,
以r为半径的圆的面积为:S=πr2.
把AB分成两条相等的线段,每个小圆的面积S2=π×(
r)2=
πr2=
S;
把AB分成三条相等的线段,每个小圆的面积S3=
πr2=
S;
把AB分成n条相等的线段,每个小圆的面积Sn=
S.
故答案为:相等.
把AB分成三条相等的线段,每个小圆的周长L3=
| 1 |
| 3 |
| 1 |
| 3 |
故答案为:
| 1 |
| 3 |
(3)把AB分成n条相等的线段,每个小圆的周长Ln=
| 1 |
| n |
| 1 |
| n |
故答案为:
| 1 |
| n |
(4)把AB分成n条不相等的线段,记n个小圆的周长分别为Cl,C2,…,Cn,
则n个小圆的周长为:2π(r1+r2+…+rn)=2πr,
大圆的周长的关系为:2πr,
故n个小圆的周长与大圆的周长的关系为:相等,
以r为半径的圆的面积为:S=πr2.
把AB分成两条相等的线段,每个小圆的面积S2=π×(
| 1 |
| 2 |
| 1 |
| 4 |
| 1 |
| 22 |
把AB分成三条相等的线段,每个小圆的面积S3=
| 1 |
| 32 |
| 1 |
| 32 |
把AB分成n条相等的线段,每个小圆的面积Sn=
| 1 |
| n2 |
故答案为:相等.
点评:此题主要考查了图形的变化类,将每个特殊的圆的面积计算出来,通过总结规律得出一般公式是解题关键.

练习册系列答案
 一课一练课时达标系列答案
一课一练课时达标系列答案
相关题目
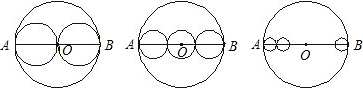
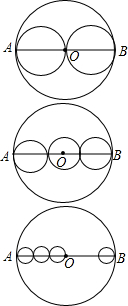 如图,AB是⊙O的直径,把AB分成几条相等的线段,以每条线段为直径分别画小圆,设AB=a,那么⊙O的周长l=πa.
如图,AB是⊙O的直径,把AB分成几条相等的线段,以每条线段为直径分别画小圆,设AB=a,那么⊙O的周长l=πa.