题目内容
【题目】如图,正方形ABCD的边长为4,延长CB至E使EB=2,以EB为边在上方作正方形EFGB,延长FG交DC于M,连接AM,AF,H为AD的中点,连接FH分别与AB,AM交于点N、K:则下列结论:①△ANH≌△GNF;②∠AFN=∠HFG;③FN=2NK;④![]() :
:![]() =1:4.其中正确的结论有( )
=1:4.其中正确的结论有( )
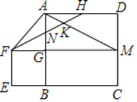
A.1个B.2个C.3个D.4个
【答案】C
【解析】
由正方形的性质得到FG=BE=2,∠FGB=90°,AD=4,AH=2,∠BAD=90°,求得∠HAN=∠FGN,AH=FG,根据全等三角形的定理定理得到△ANH≌△GNF(AAS),故①正确;根据全等三角形的性质得到∠AHN=∠HFG,推出∠AFH≠∠AHF,得到∠AFN≠∠HFG,故②错误;根据全等三角形的性质得到AN=![]() AG=1,根据相似三角形的性质得到∠AHN=∠AMG,根据平行线的性质得到∠HAK=∠AMG,根据直角三角形的性质得到FN=2NK;故③正确;根据矩形的性质得到DM=AG=2,根据三角形的面积公式即可得到结论.
AG=1,根据相似三角形的性质得到∠AHN=∠AMG,根据平行线的性质得到∠HAK=∠AMG,根据直角三角形的性质得到FN=2NK;故③正确;根据矩形的性质得到DM=AG=2,根据三角形的面积公式即可得到结论.
∵四边形EFGB是正方形,EB=2,
∴FG=BE=2,∠FGB=90°,
∵四边形ABCD是正方形,H为AD的中点,
∴AD=4,AH=2,
∠BAD=90°,
∴∠HAN=∠FGN,AH=FG,
∵∠ANH=∠GNF,
∴△ANH≌△GNF(AAS),故①正确;
∴∠AHN=∠HFG,
∵AG=FG=2=AH,
∴AF=![]() FG=
FG=![]() AH,
AH,
∴∠AFH≠∠AHF,

∴∠AFN≠∠HFG,故②错误;
∵△ANH≌△GNF,
∴AN=![]() AG=1,
AG=1,
∵GM=BC=4,
∴![]() =2,
=2,
∵∠HAN=∠AGM=90°,
∴△AHN∽△GMA,
∴∠AHN=∠AMG,
∵AD∥GM,
∴∠HAK=∠AMG,
∴∠AHK=∠HAK,
∴AK=HK,
∴AK=HK=NK,
∵FN=HN,
∴FN=2NK;故③正确;
∵延长FG交DC于M,
∴四边形ADMG是矩形,
∴DM=AG=2,
∵S△AFN=![]() ANFG=
ANFG=![]() ×2×1=1,S△ADM=
×2×1=1,S△ADM=![]() ADDM=
ADDM=![]() ×4×2=4,
×4×2=4,
∴S△AFN:S△ADM=1:4故④正确,
故选:C.

【题目】汽车刹车后,还会继续向前滑行一段距离,这段距离称为“刹车距离”刹车距离y(m)与刹车时的车速x(km/h)的部分关系如表:
刹车时的车速 | 0 | 50 | 100 | 200 |
刹车距离 | 0 | 5.5 | 46.5 | 82 |
(1)求出y与x之间的函数关系式.
(2)一辆车在限速120km/h的高速公路上行驶时出了事故,事后测得它的刹车距离为40.6m,问:该车在发生事故时是否超速行驶?