题目内容
关于x的方程:x+ =c+
=c+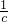 的解是x1=c,x2=
的解是x1=c,x2=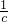 ;
;
x- =c-
=c-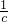 (即x+
(即x+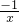 =c+
=c+ )的解是x1=c,x2=-
)的解是x1=c,x2=-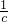 ;
;
x+ =c+
=c+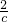 的解是:x1=c,x2=
的解是:x1=c,x2=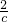 ,…
,…
(1)观察上述方程及其解的特征,直接写出关于x的方程x+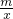 =c+
=c+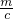 (m≠0)的解,并利用“方程的解”的概念进行验证;
(m≠0)的解,并利用“方程的解”的概念进行验证;
(2)通过(1)的验证所获得的结论,你能解出关于x的方程:x+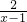 =a+
=a+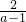 的解吗?若能,请求出此方程的解;若不能,请说明理由.
的解吗?若能,请求出此方程的解;若不能,请说明理由.
解:(1)x1=c,x2=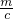 ;
;
把x1=c代入方程,得
左=c+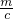 ,右=c+
,右=c+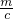 ,
,
∴左=右.
把x2=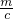 代入方程,得
代入方程,得
左=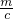 +c,右=c+
+c,右=c+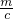
∴左=右.
∴x1=c,x2=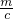 是关于x的方程x+
是关于x的方程x+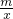 =c+
=c+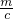 的解.
的解.
(2)x+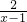 =a+
=a+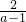
两边同时减1变形为x-1+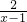 =a-1+
=a-1+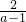
∴x-1=a-1 x-1=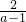
∴x1=a,x2=1+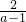 ,即x2=
,即x2=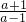 .
.
分析:(1)本题可根据给出的方程的解的概念,来求出所求的方程的解.
(2)本题要求的方程和题目给出的例子中的方程形式不一致,可先将所求的方程进行变形.变成式子中的形式后再根据给出的规律进行求解.
点评:本题要注意给出的例子中的方程与解的规律,还要注意套用列子中的规律时,要保证所求方程与例子中的方程的形式一致.
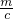 ;
;把x1=c代入方程,得
左=c+
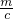 ,右=c+
,右=c+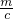 ,
,∴左=右.
把x2=
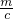 代入方程,得
代入方程,得左=
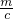 +c,右=c+
+c,右=c+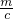
∴左=右.
∴x1=c,x2=
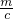 是关于x的方程x+
是关于x的方程x+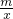 =c+
=c+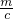 的解.
的解.(2)x+
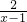 =a+
=a+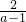
两边同时减1变形为x-1+
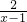 =a-1+
=a-1+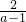
∴x-1=a-1 x-1=
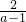
∴x1=a,x2=1+
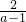 ,即x2=
,即x2=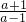 .
.分析:(1)本题可根据给出的方程的解的概念,来求出所求的方程的解.
(2)本题要求的方程和题目给出的例子中的方程形式不一致,可先将所求的方程进行变形.变成式子中的形式后再根据给出的规律进行求解.
点评:本题要注意给出的例子中的方程与解的规律,还要注意套用列子中的规律时,要保证所求方程与例子中的方程的形式一致.

练习册系列答案
相关题目