题目内容
直角△ABC的三边a、b、c均满足关于x的方程x2-mx+| 2 |
分析:因为一元二次方程最多有两个不相等的实数根,而直角△ABC的三边a、b、c均满足方程,则该直角三角形一定是等腰直角三角形.根据等腰直角三角形的斜边是直角边的
倍,可以求得方程的两个根,其中较小的根是等腰直角三角形的直角边,进一步求得三角形的面积即可.
| 2 |
解答:解:根据题意,得
该直角三角形是等腰直角三角形,则斜边是直角边的
倍.
设方程的较小的根是x,则较大的根是
x.根据根与系数的关系,得
x•
x=
,
解得x=±1(负值舍去).
则直角三角形的直角边是1,直角三角形的面积是
.
该直角三角形是等腰直角三角形,则斜边是直角边的
| 2 |
设方程的较小的根是x,则较大的根是
| 2 |
x•
| 2 |
| 2 |
解得x=±1(负值舍去).
则直角三角形的直角边是1,直角三角形的面积是
| 1 |
| 2 |
点评:此题综合考查了等腰直角三角形的性质和一元二次方程根与系数的关系.

练习册系列答案
相关题目
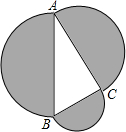 如图,分别以直角△ABC的三边AB、BC、CA为直径向外作半圆,设直线AB左边阴影部分面积为S1,右边阴影部分面积为S2,则( )
如图,分别以直角△ABC的三边AB、BC、CA为直径向外作半圆,设直线AB左边阴影部分面积为S1,右边阴影部分面积为S2,则( )| A、S1=S2 | B、S1<S2 | C、S1>S2 | D、无法确定 |
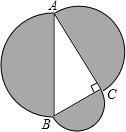 如图,分别以直角△ABC的三边AB,BC,CA为直径向外作半圆.设直线AB左边阴影部分的面积为S1,右边阴影部分的面积和为S2,则S1
如图,分别以直角△ABC的三边AB,BC,CA为直径向外作半圆.设直线AB左边阴影部分的面积为S1,右边阴影部分的面积和为S2,则S1 探究题
探究题