Question

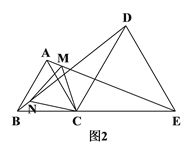
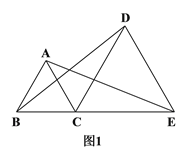
【题目】如图，等腰三角形ABC中，P为底边BC上任意点，过P作两腰的平行线分别与AB，AC相交于Q，R两点，又P′是P关于直线RQ的对称点，证明：P′在△ABC的外接圆上．

Answer 1

【答案】证明见解析.

【解析】

先利用四边形ARPQ为平行四边形，根据同弧所对圆周角相等，证明P'，A，R，Q四点共圆,再证明∠AP'B和∠BCA互补，证明 ABCP'四点共圆.

证明：连接P'Q，P'A，QR，BP′，

∵QP∥AC，PR∥AB

∴四边形ARPQ为平行四边形

∴∠QAR=∠RPQ，

由对称关系得到，∠RPQ=∠RP'Q，

所以∠QAR=∠QP'R，

所以P'，A，R，Q四点共圆，

∴∠QP'R=∠BAC,

同理得到∠QBP'=∠QP'B，∠RP'A=∠BAP',

∴可以得到∠AP'B+∠BCA =180度，所以ABCP'四点共圆，

∴P′在△ABC的外接圆上．