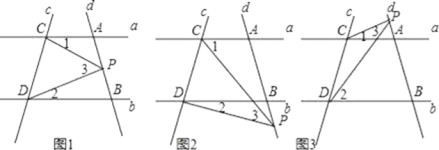
��Ŀ����
����Ŀ����ͼ����ƽ��ֱ������ϵ�У�������y=mx2+4mx��5m��m��0����x�ύ�ڵ�A��B����A�ڵ�B����ࣩ���������ߵĶԳ�����ֱ��y= ![]() x�ཻ�ڵ�E����x���ཻ�ڵ�D����P��ֱ��y=
x�ཻ�ڵ�E����x���ཻ�ڵ�D����P��ֱ��y= ![]() x�ϣ�����ԭ���غϣ�������PD������P��PF��PD��y���ڵ�F������DF��
x�ϣ�����ԭ���غϣ�������PD������P��PF��PD��y���ڵ�F������DF�� 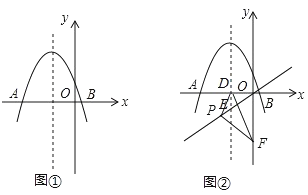
��1����ͼ����ʾ���������߶����������Ϊ6 ![]() ���������ߵĽ���ʽ��
���������ߵĽ���ʽ��
��2����A��B��������ꣻ
��3����ͼ����ʾ��С����̽����P��λ�÷��֣�����P���E�غ�ʱ����PDF�Ĵ�СΪ��ֵ���������룺����ֱ��y= ![]() x������һ��P������ԭ���غϣ�����PDF�Ĵ�СΪ��ֵ�������жϸò����Ƿ���ȷ����˵�����ɣ�
x������һ��P������ԭ���غϣ�����PDF�Ĵ�СΪ��ֵ�������жϸò����Ƿ���ȷ����˵�����ɣ�
���𰸡�
��1��
�⣺��y=mx2+4mx��5m��
��y=m��x2+4x��5��=m��x+5����x��1����
��y=0�ã�m��x+5����x��1��=0��
��m��0��
��x=��5��x=1��
��A����5��0����B��1��0����
�������ߵĶԳ���Ϊx=��2��
�������ߵĶ�������ΪΪ6 ![]() ��
��
�ੁ9m=6 ![]() ��
��
��m=�� ![]() ��
��
�������ߵĽ���ʽΪy=�� ![]() x2��
x2�� ![]() x+
x+ ![]()
��2��
�⣺�ɣ�1����֪��A����5��0����B��1��0��
��3��
�⣺��ͼ��ʾ��
��OP�Ľ���ʽΪy= ![]() x��
x��
���AOP=30�㣮
���PBF=60��
��PD��PF��FO��OD��
���DPF=��FOD=90�㣮
���DPF+��FOD=180�㣮
���O��D��P��F��Բ��
���PDF=��PBF��
���PDF=60�㣮
����������1������ȡ��ʽ��ʽ��ԭʽ����Ϊy=m��x2+4x��5����Ȼ����y=0����ú���ͼ����x��Ľ������꣬�Ӷ�����õ�A��B�����꣬Ȼ�����������ߵĶԳ��Կɵõ������ߵĶԳ���Ϊx=��2���ʴ˿�֪��x=��2ʱ��y=6 ![]() �����ǿ����m��ֵ����2���ɣ�1���Ŀ�֪��A��B�����꣨3������һ�κ����Ľ���ʽ�õ���PBF�Ķ�����Ȼ������PD��PF��FO��OD��֤����O��D��P��F��Բ���������Բ�ܽǶ�����֤����PDF=60�㣮������Ҫ������Ƕ��κ��������ʡ���һԪ���η��̡�����ͼ����������Ľ��㣬�ĵ㹲Բ��Բ�ܽǶ�����Ӧ�ã�֤�õ�O��D��P��F��Բ�ǽ���Ĺؼ���
�����ǿ����m��ֵ����2���ɣ�1���Ŀ�֪��A��B�����꣨3������һ�κ����Ľ���ʽ�õ���PBF�Ķ�����Ȼ������PD��PF��FO��OD��֤����O��D��P��F��Բ���������Բ�ܽǶ�����֤����PDF=60�㣮������Ҫ������Ƕ��κ��������ʡ���һԪ���η��̡�����ͼ����������Ľ��㣬�ĵ㹲Բ��Բ�ܽǶ�����Ӧ�ã�֤�õ�O��D��P��F��Բ�ǽ���Ĺؼ���
�����㾫����������ʽ�ֽⷨ�Ͷ��κ����������ǽ����ĸ�������Ҫ֪����֪δ֪�ȷ��룬��ʽ�ֽ�����Σ�����ϵ���Ȼ������Ͳ�����ʽ����ȫƽ���ȳ���������䷽�����ƣ������ԣ���a>0ʱ���Գ�����ߣ�y��x�������С���Գ����ұߣ�y��x���������a<0ʱ���Գ�����ߣ�y��x��������Գ����ұߣ�y��x�������С��

����Ŀ��Ϊ�˽��п�������ϲ�����������͵�Ӣ����⣬2015��־Ը�߱���ȫ���п��������Ӣ�����ġ��������֡�����ѡ��������ա��Ķ����⡢����Ӧ�á��������ʾ����飬Ҫ��ÿλ����������ѡ������һ�����ͣ�Ϊ����������˸����㲿�ֿ��������������������Ƴ���ͼ��ͳ��ͼ�����ʾ�������Ϊ100%������Ϊ��Ч�ʾ�����
�����鿼��ѡ������ͳ�Ʊ�
���� | ��ռ�ٷֱ� |
�������� | a |
����ѡ�� | 35% |
������� | b |
�Ķ����� | 10% |
����Ӧ�� | c |
����ͳ��ͼ���е���Ϣ������������⣺
��1���α�����Ŀ�����������a��b��c��ֵ��
��2��������ͳ��ͼ����������
��3��ȫ�вμ�����п��Ŀ�������42000�ˣ��Թ���ȫ�п�������ϲ����������ѡ���������Ŀ����ж����ˣ�
����Ŀ������ˮ��˾�����������û�������ˮ��x����λ���֣���������ˮ�����û��ֳ�A��B��C��D��E�������ͳ�ƣ�����������ͼ��ʾ������ͳ��ͼ����֪��B�����⣬���������û���64���������в��������û�������ˮ����6�����µĹ��У�������
��� | ����ˮ��x����λ���֣� |
A | 0��x��3 |
B | 3��x��6 |
C | 6��x��9 |
D | 9��x��12 |
E | x��12 |

A.18��
B.20��
C.22��
D.24��