题目内容
【题目】如图，已知抛物线y=ax2+bx+3经过点B（﹣1，0）、C（3，0），交y轴于点A，将线段OB绕点O顺时针旋转90°，点B的对应点为点M，过点A的直线与x轴交于点D（4，0）．直角梯形EFGH的上底EF与线段CD重合，∠FEH=90°，EF∥HG，EF=EH=1．直角梯形EFGH从点D开始，沿射线DA方向匀速运动，运动的速度为1个长度单位/秒，在运动过程中腰FG与直线AD始终重合，设运动时间为t秒．
（1）求此抛物线的解析式；
（2）当t为何值时，以M、O、H、E为顶点的四边形是特殊的平行四边形；
（3）作点A关于抛物线对称轴的对称点A′，直线HG与对称轴交于点K，当t为何值时，以A、A′、G、K为顶点的四边形为平行四边形？请直接写出符合条件的t值．
【答案】
（1）
解：∵抛物线y=ax2+bx+3经过点B（﹣1，0）、C（3，0），
∴ 
，解得a=﹣1，b=2，
∴抛物线的解析式为：y=﹣x2+2x+3．
（2）
解：在直角梯形EFGH运动的过程中：
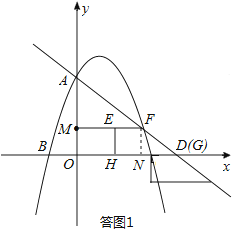
①四边形MOHE构成矩形的情形，如答图1所示：
此时边GH落在x轴上时，点G与点D重合．
由题意可知，EH，MO均与x轴垂直，且EH=MO=1，则此时四边形MOHE构成矩形．此时直角梯形EFGH平移的距离即为线段DF的长度．
过点F作FN⊥x轴于点N，则有FN=EH=1，FN∥y轴，
∴ 
，即 
，解得DN= 
．
在Rt△DFN中，由勾股定理得：DF= 
= 
= 
，
∴t= ；
②四边形MOHE构成正方形的情形．
由答图1可知，
OH=OD﹣DN﹣HN=4﹣ ﹣1= ，即OH≠MO，
所以此种情形不存在；
③四边形MOHE构成菱形的情形，如答图2所示：
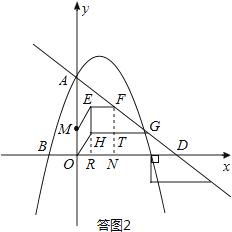
过点F作FN⊥x轴于点N，交GH于点T，过点H作HR⊥x轴于点R．易知FN∥y轴，RN=EF=FT=1，HR=TN．
设HR=x，则FN=FT+TN=FT+HR=1+x；
∵FN∥y轴，∴ ，即 
，解得DN= （1+x）．
∴OR=OD﹣RN﹣DN=4﹣1﹣ （1+x）= ﹣ x．
若四边形MOHE构成菱形，则OH=EH=1，
在Rt△ORH中，由勾股定理得：OR2+HR2=OH2，
即：（ ﹣ x）2+x2=12，解得x= 
，
∴FN=1+x= 
，DN= （1+x）= 
．
在Rt△DFN中，由勾股定理得：DF= = 
=3．
由此可见，四边形MOHE构成菱形的情形存在，此时直角梯形EFGH平移的距离即为线段DF的长度，
∴t=3．
综上所述，当t= s时，四边形MOHE构成矩形；当t=3s时，四边形MOHE构成菱形
（3）
解：当t= 
s或t= 
s时，以A、A′、G、K为顶点的四边形为平行四边形．
简答如下：（注：本题并无要求写出解题过程，以下仅作参考）
由题意可知，AA′=2．以A、A′、G、K为顶点的四边形为平行四边形，则GK∥AA′，且GK=AA′=2．
①当直角梯形位于△OAD内部时，如答图3所示：
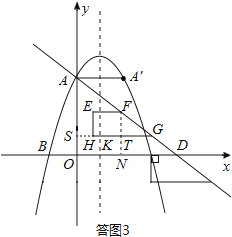
过点H作HS⊥y轴于点S，由对称轴为x=1可得KS=1，∴SG=KS+GK=3．
由SG∥x轴，得 
，求得AS= 
，∴OS=OA﹣AS= 
，
∴FN=FT+TN=FT+OS= 
，易知DN= FN= 
，
在Rt△FND中，由勾股定理求得DF= ；
②当直角梯形位于△OAD外部时，如答图4所示：
设GK与y轴交于点S，则GS=SK=1，AS= ，OS=OA+AS= 
．
过点F作FN⊥x轴，交GH于点T，则FN=FT+NT=FT+OS= 
．
在Rt△FGT中，FT=1，则TG= ，FG= ．
由TG∥x轴，∴ 
，解得DF= ．
由于在以上两种情形中，直角梯形EFGH平移的距离均为线段DF的长度，则综上所述，当t= s或t= s时，以A、A′、G、K为顶点的四边形为平行四边形．
【解析】（1）利用待定系数法求出抛物线的解析式；（2）在直角梯形的平移过程中，四边形MOHE可能构成矩形（如答图1所示），或菱形（如答图2所示）；本问有两种情形，需要分类求解，注意不要漏解，而且需要排除正方形的情形；（3）本问亦有两种情形，需要分类求解．当直角梯形运动到△OAD内部的情形时，如答图3所示；当直角梯形运动到△OAD外部的情形时，如答图4所示．
