题目内容
【题目】如图,已知△ABC中,∠ABC=90°,AB=BC,三角形的顶点在相互平行的三条直线l1 , l2 , l3上,且l1 , l2之间的距离为2,l2 , l3之间的距离为3,则AC的长是( ) 
A.![]()
B.![]()
C.![]()
D.7
【答案】A
【解析】解:作AD⊥l3于D,作CE⊥l3于E, 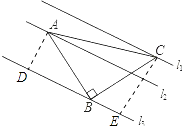
∵∠ABC=90°,
∴∠ABD+∠CBE=90°
又∠DAB+∠ABD=90°
∴∠BAD=∠CBE,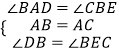 ,
,
∴△ABD≌△BCE
∴BE=AD=3
在Rt△BCE中,根据勾股定理,得BC= ![]() =
= ![]() ,
,
在Rt△ABC中,根据勾股定理,得AC= ![]() ×
× ![]() =2
=2 ![]() ;
;
故选A.
【考点精析】利用全等三角形的性质和勾股定理的概念对题目进行判断即可得到答案,需要熟知全等三角形的对应边相等; 全等三角形的对应角相等;直角三角形两直角边a、b的平方和等于斜边c的平方,即;a2+b2=c2.

练习册系列答案
相关题目
【题目】八(2)班组织了一次经典朗读比赛,甲、乙两队各10人的比赛成绩如表(10分制):
甲 | 7 | 8 | 9 | 7 | 10 | 10 | 9 | 10 | 10 | 10 |
乙 | 10 | 8 | 7 | 9 | 8 | 10 | 10 | 9 | 10 | 9 |
(1)甲队成绩的中位数是分,乙队成绩的众数是分;
(2)计算甲、乙队的平均成绩和方差,试说明成绩较为整齐的是哪一队?

