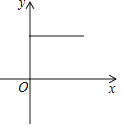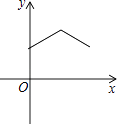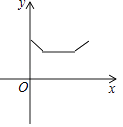Question

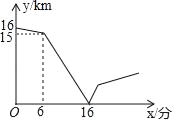
【题目】甲、乙两人在一条笔直的道路上相向而行，甲骑自行车从A地到B地，乙驾车从B地到A地，他们分别以不同的速度匀速行驶，已知甲先出发6分钟后，乙才出发，在整个过程中，甲、乙两人的距离y（km）与甲出发的时间x（分）之间的关系如图所示．

（1）求甲、乙相遇时，乙所行驶的路程；

（2）当乙到达终点A时，甲还需多少分钟到达终点B？

Answer 1

【答案】（1）千米；（2）78分钟.

【解析】

（1）根据路程与时间的关系，可得甲、乙的速度，再根据甲、乙相遇时，乙所行驶的路程=10×乙的速度，即可解答；（2）根据相遇前甲行驶的路程除以乙行驶的速度，可得乙到达A站需要的时间，根据相遇前乙行驶的路程除以甲行驶的速度，可得甲到达B站需要的时间，再根据有理数的减法，可得结果．

（1）由纵坐标看出甲先行驶了1千米，由横坐标看出甲行驶1千米用了6分钟，

甲的速度是1÷6=千米/分钟，

由纵坐标看出AB两地的距离是16千米，

设乙的速度是x千米/分钟，由题意，得:

10x+16×=16，

解得x=千米/分钟，

∴甲、乙相遇时，乙所行驶的路程：10×=（千米）

（2）相遇后乙到达A站还需（16×）÷=2分钟，

相遇后甲到达B站还需（10×）÷=80分钟，

当乙到达终点A时，甲还需80﹣2=78分钟到达终点B．