题目内容
【题目】在平面直角坐标系xOy中,点P和点P'关于y=x轴对称,点Q和点P'关于R(a,0)中心对称,则称点Q是点P关于y=x轴,点R(a,0)的“轴中对称点”.
(1)如图1,已知点A(0,1).
①若点B是点A关于y=x轴,点G(3,0)的“轴中对称点”,则点B的坐标为 ;
②若点C(-3,0)是点A关于y=x轴,点R(a,0)的“轴中对称点”,则a= ;
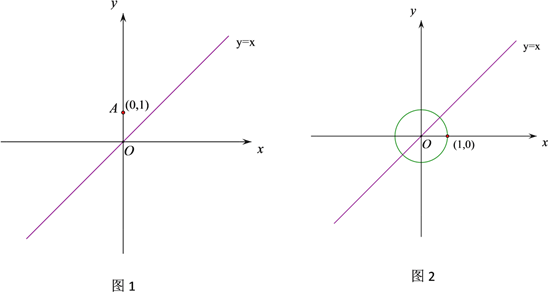
(2)如图2,⊙O的半径为1,若⊙O上存在点M,使得点M'是点M关于y=x轴,点T(b,0)的“轴中对称点”,且点M'在射线y=x-4(x![]() 4)上.
4)上.
①⊙O上的点M关于y=x轴对称时,对称点组成的图形是 ;
②求b的取值范围;
(3)⊙E的半径为2,点E(0,t)是y轴上的动点,若⊙E上存在点N,使得点N'是点N关于y=x轴,点(2,0)的“轴中对称点”,并且N'在直线![]() 上,请直接写出t的取值范围.
上,请直接写出t的取值范围.

【答案】(1)① B(5,0);②a=-1;(2)① 圆;②![]() ;(3)
;(3)![]()
【解析】解:(1)① B(5,0).
②a=-1.
(2)① 圆.
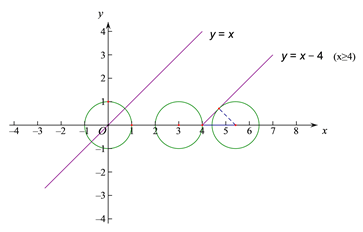
②当以1为半径的圆过(4,0)时,圆心坐标(3,0).
∴![]() .
.
当以1为半径的圆与射线y=x-4相切时,
圆心坐标(![]() ,0).
,0).
∴![]() .
.
∴![]() .
.
(3)![]() .
.

练习册系列答案
相关题目