题目内容
【题目】如图

如图1,四边形ABCD和四边形BCMD都是菱形,
(1)求证:∠M=60°
(2)如图2,点E在边AD上,点F在边CM上,连接EF交CD于点H,若AE=MF,求证:EH=HF;
(3)如图3,在第(2)小题的条件下,连接BH,若EF⊥CM,AB=3,求BH的长
【答案】(1)证明见解析 (2)证明见解析 (3)![]()
【解析】
(1)利用菱形的四条边相等,可证CD=DM=CM=AD,就可得到△CDM是等边三角形,再利用等边三角形的三个角都是60°,就可求出∠M的度数;
(2)过点E作EG∥CM交CD的延长线于点G,可得到∠G=∠HCF,先证明△EDG是等边三角形,结合已知条件证明EG=CF,利用AAS证明△EGH≌△FCH,再根据全等三角形的对应边相等,可证得结论;
(3)设BD,EF交于点N,根据前面的证明可知BD=CD=AB=3,∠M=∠CDM=60°,DE=CF,再利用垂直的定义及三角形内角和定理可求出∠HED,∠EHD的度数,从而利用等腰三角形的判定和性质,可证得ED=DH=CF,可推出CD=3DH,就可求出DH的长,然后利用解直角三角形分别求出BN,NH的长,再利用勾股定理就可求出BH的长.
(1)证明:∵ 四边形ABCD和四边形BCMD都是菱形,
∴BC=CD=AD,BC=DM=CM
∴CD=DM=CM=AD,
∴△CDM是等边三角形,
∴∠M=60°。
(2)解: 如图2,过点E作EG∥CM交CD的延长线于点G,

∴∠G=∠HCF=60°,∠GED=∠M=60°,
∴∠G=∠GED=∠EDG=60°,
∴△EDG是等边三角形
∴EG=DE;
∵AD=CM,AE=MF,
∴DE=CF,
∴EG=CF;
在△EGH和△FCH中,

∴△EGH≌△FCH(AAS)
∴EH=FH.
(3)解: 如图3,设BD,EF交于点N,

由(1)(2)的证明过程可知BD=CD=AB=3,∠M=∠CDM=60°,DE=CF,
∵EF⊥CM,
∴∠EFM=90°,
∴∠HED=90°-60°=30°,
∠CDM=∠HED+∠EHD=60°
∴∠EHD=60°-30°=30°=∠HED=∠CHF
∴ED=DH=CF,
在R△CHF中,∠CHF=30°
∴CH=2CH=2DH,
∴CD=CH+DH=3DH=3
解之:DH=CF=1
∵菱形CBDM,EF⊥CM
∴BD∥CM
∴EF⊥BD;
∴∠DNH=∠BNH=90°,
在Rt△DHN中,∠DHN=30°,DH=1
∴DN=DHsin∠30°=![]() ,
,
NH=DHcos30°=![]() ;
;
∴BN=BD-DN=3-![]() =
=![]() ,
,
在Rt△BHN中,
BH=![]() .
.

【题目】我乡某校举行全体学生“定点投篮”比赛,每位学生投40个,随机抽取了部分学生的投篮结果,并绘制成如下统计图表。
组别 | 投进个数 | 人数 |
A |
| 10 |
B |
| 15 |
C |
| 30 |
D |
| m |
E |
| n |
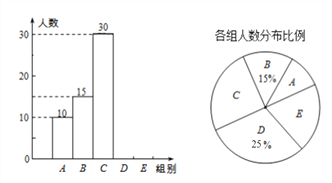
根据以上信息完成下列问题。
①本次抽取的学生人数为多少?
②统计表中的m=__________;
③扇形统计图中E组所占的百分比;
④补全频数分布直方图;
⑤扇形统计图中“C组”所对应的圆心角的度数;
⑥本次比赛中投篮个数的中位数落在哪一组;
⑦已知该校共有900名学生,如投进个数少于24个定为不合格,请你估计该校本次投篮比赛不合格的学生人数.





