题目内容
阅读下列材料:一个直角三角形纸片ABC,分别取AB、AC边的中点M、N,连接MN,作∠AHM=∠AHN=90°,将三角形纸片沿AH、MN剪开分割成三块,如图1所示;如图2,将三角形纸片①绕AB的中点M旋转至三角形纸片④处,将三角形纸片②绕AC的中点N旋转至三角形纸片⑤处,依此方法操作,可以把直角三角形纸片ABC拼接成一个与它面积相等的长方形纸片DBCE.
解决下列问题:
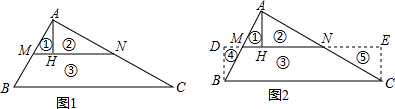
(1)如图3,一个任意三角形纸片ABC,将其分割后拼接成一个与三角形ABC的面积相等的长方形,在图3中画出分割的实线和拼接的虚线;
(2)如图4,一个任意四边形纸片ABCD,将其分割后拼接成一个与四边形ABCD的面积相等的长方形,在图4画出分割的实线和拼接的虚线.
解决下列问题:

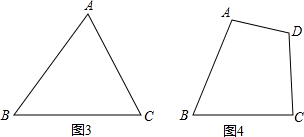
(1)如图3,一个任意三角形纸片ABC,将其分割后拼接成一个与三角形ABC的面积相等的长方形,在图3中画出分割的实线和拼接的虚线;
(2)如图4,一个任意四边形纸片ABCD,将其分割后拼接成一个与四边形ABCD的面积相等的长方形,在图4画出分割的实线和拼接的虚线.

分析:(1)过两边的中点垂直于第三边剪开,再把得到的两个小直角三角形进行拼接即可得到一矩形;
(2)先连接四边形的一条对角线把四边形分成两个三角形,然后沿两三角形平行于连接的四边形的对角线的中位线剪开,再把剪开得到的小三角形垂直于剪开的边过顶点剪开,进行拼接即可得到一矩形.
(2)先连接四边形的一条对角线把四边形分成两个三角形,然后沿两三角形平行于连接的四边形的对角线的中位线剪开,再把剪开得到的小三角形垂直于剪开的边过顶点剪开,进行拼接即可得到一矩形.
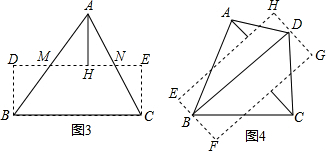
解答:解:(1)如图3所示:
(2)如图4所示:
 .
.
(2)如图4所示:
 .
.点评:此题主要考查了图形的剪拼,准确理解三角形与矩形的关系,考虑剪开后出现直角是关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
、阅读下列材料并填空。平面上有n个点(n≥2)且任意三个点不在同一条直线上,过这些点作直线,一共能作出多少条不同的直线?
①分析:当仅有两个点时,可连成1条直线;当有3个点时,可连成3条直线;当有4个点时,可连成6条直线;当有5个点时,可连成10条直线……
②归纳:考察点的个数和可连成直线的条数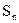 发现:如下表
发现:如下表
③推理:平面上有n个点,两点确定一条直线。取第一个点A有n种取法,取第二个点B有(n-1)种取法,所以一共可连成n(n-1)条直线,但AB与BA是同一条直线,故应除以2;即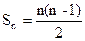
④结论: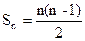
试探究以下几个问题:平面上有n个点(n≥3),任意三个点不在同一条直线上,过任意三个点作三角形,一共能作出多少不同的三角形?
(1)分析:
当仅有3个点时,可作出 个三角形;
当仅有4个点时,可作出 个三角形;
当仅有5个点时,可作出 个三角形;
……
(2)归纳:考察点的个数n和可作出的三角形的个数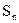 ,发现:(填下表)
,发现:(填下表)
(3)推理:
(4)结论:
①分析:当仅有两个点时,可连成1条直线;当有3个点时,可连成3条直线;当有4个点时,可连成6条直线;当有5个点时,可连成10条直线……
②归纳:考察点的个数和可连成直线的条数
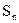 发现:如下表
发现:如下表| 点的个数 | 可作出直线条数 |
| 2 | 1=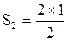 |
| 3 | 3=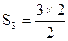 |
| 4 | 6=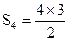 |
| 5 | 10=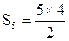 |
| …… | …… |
| n | 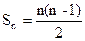 |
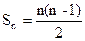
④结论:
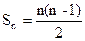
试探究以下几个问题:平面上有n个点(n≥3),任意三个点不在同一条直线上,过任意三个点作三角形,一共能作出多少不同的三角形?
(1)分析:
当仅有3个点时,可作出 个三角形;
当仅有4个点时,可作出 个三角形;
当仅有5个点时,可作出 个三角形;
……
(2)归纳:考察点的个数n和可作出的三角形的个数
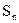 ,发现:(填下表)
,发现:(填下表)| 点的个数 | 可连成三角形个数 |
| 3 | |
| 4 | |
| 5 | |
| …… | |
| n | |
(3)推理:
(4)结论:
阅读下列材料并填空。平面上有n个点(n≥2)且任意三个点不在同一条直线上,过这些点作直线,一共能作出多少条不同的直线?
(1)分析:当仅有两个点时,可连成1条直线;当有3个点时,可连成3条直线;当有4个点时,可连成6条直线;当有5个点时,可连成10条直线……
(2)归纳:考察点的个数和可连成直线的条数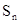 发现:如下表
发现:如下表
| 点的个数 | 可作出直线条数 |
| 2 | 1=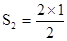 |
| 3 | 3=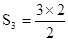 |
| 4 | 6=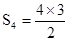 |
| 5 | 10=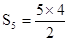 |
| …… | …… |
| n | 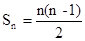 |
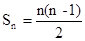
(4)结论:
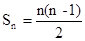
试探究以下几个问题:平面上有n个点(n≥3),任意三个点不在同一条直线上,过任意三个点作三角形,一共能作出多少不同的三角形?
(1)分析:
当仅有3个点时,可作出 个三角形;
当仅有4个点时,可作出 个三角形;
当仅有5个点时,可作出 个三角形;
……
(2)归纳:考察点的个数n和可作出的三角形的个数
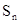 ,发现:(填下表)
,发现:(填下表)| 点的个数 | 可连成三角形个数 |
| 3 | |
| 4 | |
| 5 | |
| …… | |
| n | |
、阅读下列材料并填空。平面上有n个点(n≥2)且任意三个点不在同一条直线上,过这些点作直线,一共能作出多少条不同的直线?
①分析:当仅有两个点时,可连成1条直线;当有3个点时,可连成3条直线;当有4个点时,可连成6条直线;当有5个点时,可连成10条直线……
②归纳:考察点的个数和可连成直线的条数 发现:如下表
发现:如下表
| 点的个数 | 可作出直线条数 |
| 2 | 1=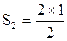 |
| 3 | 3=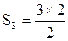 |
| 4 | 6=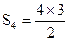 |
| 5 | 10=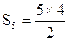 |
| …… | …… |
| n | 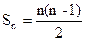 |
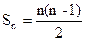
④结论:
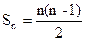
试探究以下几个问题:平面上有n个点(n≥3),任意三个点不在同一条直线上,过任意三个点作三角形,一共能作出多少不同的三角形?
(1)分析:
当仅有3个点时,可作出 个三角形;
当仅有4个点时,可作出 个三角形;
当仅有5个点时,可作出 个三角形;
……
(2)归纳:考察点的个数n和可作出的三角形的个数
 ,发现:(填下表)
,发现:(填下表)| 点的个数 | 可连成三角形个数 |
| 3 | |
| 4 | |
| 5 | |
| …… | |
| n | |
(3)推理:
(4)结论:
阅读下列材料并填空.
平面上有n个点(n≥2)且任意三个点不在同一条直线上,过其中的每两点画直线,一共能作出多少条不同的直线?
①分析:当仅有两个点时,可连成1条直线;当有3个点时,可连成3条直线;当有4个点时,可连成6条直线;当有5个点时,可连成10条直线…
②归纳:考察点的个数和可连成直线的条数Sn发现:如下表
③推理:平面上有n个点,两点确定一条直线.取第一个点A有n种取法,取第二个点B有(n-1)种取法,所以一共可连成n(n-1)条直线,但AB与BA是同一条直线,故应除以2;即Sn=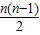 ④结论:Sn=
④结论:Sn=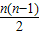 试探究以下几个问题:平面上有n个点(n≥3),任意三个点不在同一条直线上,过任意三个点作三角形,一共能作出多少不同的三角形?
试探究以下几个问题:平面上有n个点(n≥3),任意三个点不在同一条直线上,过任意三个点作三角形,一共能作出多少不同的三角形?
(1)分析:
当仅有3个点时,可作出______个三角形;
当仅有4个点时,可作出______个三角形;
当仅有5个点时,可作出______个三角形;
…
(2)归纳:考察点的个数n和可作出的三角形的个数Sn,发现:(填下表)
(3)推理:
(4)结论:
平面上有n个点(n≥2)且任意三个点不在同一条直线上,过其中的每两点画直线,一共能作出多少条不同的直线?
①分析:当仅有两个点时,可连成1条直线;当有3个点时,可连成3条直线;当有4个点时,可连成6条直线;当有5个点时,可连成10条直线…
②归纳:考察点的个数和可连成直线的条数Sn发现:如下表
| 点的个数 | 可作出直线条数 |
| 2 | 1=S2=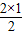 |
| 3 | 3=S3=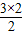 |
| 4 | 6=S4=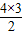 |
| 5 | 10=S5=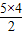 |
| … | … |
| n | Sn=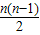 |
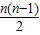 ④结论:Sn=
④结论:Sn=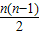 试探究以下几个问题:平面上有n个点(n≥3),任意三个点不在同一条直线上,过任意三个点作三角形,一共能作出多少不同的三角形?
试探究以下几个问题:平面上有n个点(n≥3),任意三个点不在同一条直线上,过任意三个点作三角形,一共能作出多少不同的三角形?(1)分析:
当仅有3个点时,可作出______个三角形;
当仅有4个点时,可作出______个三角形;
当仅有5个点时,可作出______个三角形;
…
(2)归纳:考察点的个数n和可作出的三角形的个数Sn,发现:(填下表)
| 点的个数 | 可连成三角形个数 |
| 3 | |
| 4 | |
| 5 | |
| … | |
| n |
(4)结论:
阅读下列材料并填空.
平面上有n个点(n≥2)且任意三个点不在同一条直线上,过其中的每两点画直线,一共能作出多少条不同的直线?
①分析:当仅有两个点时,可连成1条直线;当有3个点时,可连成3条直线;当有4个点时,可连成6条直线;当有5个点时,可连成10条直线…
②归纳:考察点的个数和可连成直线的条数Sn发现:如下表
③推理:平面上有n个点,两点确定一条直线.取第一个点A有n种取法,取第二个点B有(n-1)种取法,所以一共可连成n(n-1)条直线,但AB与BA是同一条直线,故应除以2;即Sn=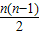 ④结论:Sn=
④结论:Sn=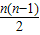 试探究以下几个问题:平面上有n个点(n≥3),任意三个点不在同一条直线上,过任意三个点作三角形,一共能作出多少不同的三角形?
试探究以下几个问题:平面上有n个点(n≥3),任意三个点不在同一条直线上,过任意三个点作三角形,一共能作出多少不同的三角形?
(1)分析:
当仅有3个点时,可作出______个三角形;
当仅有4个点时,可作出______个三角形;
当仅有5个点时,可作出______个三角形;
…
(2)归纳:考察点的个数n和可作出的三角形的个数Sn,发现:(填下表)
(3)推理:
(4)结论:
平面上有n个点(n≥2)且任意三个点不在同一条直线上,过其中的每两点画直线,一共能作出多少条不同的直线?
①分析:当仅有两个点时,可连成1条直线;当有3个点时,可连成3条直线;当有4个点时,可连成6条直线;当有5个点时,可连成10条直线…
②归纳:考察点的个数和可连成直线的条数Sn发现:如下表
| 点的个数 | 可作出直线条数 |
| 2 | 1=S2=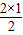 |
| 3 | 3=S3=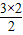 |
| 4 | 6=S4=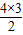 |
| 5 | 10=S5=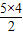 |
| … | … |
| n | Sn=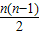 |
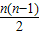 ④结论:Sn=
④结论:Sn=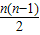 试探究以下几个问题:平面上有n个点(n≥3),任意三个点不在同一条直线上,过任意三个点作三角形,一共能作出多少不同的三角形?
试探究以下几个问题:平面上有n个点(n≥3),任意三个点不在同一条直线上,过任意三个点作三角形,一共能作出多少不同的三角形?(1)分析:
当仅有3个点时,可作出______个三角形;
当仅有4个点时,可作出______个三角形;
当仅有5个点时,可作出______个三角形;
…
(2)归纳:考察点的个数n和可作出的三角形的个数Sn,发现:(填下表)
| 点的个数 | 可连成三角形个数 |
| 3 | |
| 4 | |
| 5 | |
| … | |
| n |
(4)结论: