题目内容
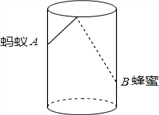
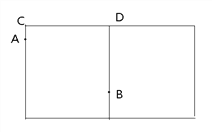
【题目】如图，圆柱形容器高为18cm，底面周长为24cm，在杯内壁离杯底4cm的点B处有一滴蜂蜜，此时一只蚂蚁正好在杯外壁，离杯上沿2cm与蜂蜜相对的点A处，为了吃到蜂蜜，蚂蚁从外壁A处沿着最短路径到达内壁B处。
（1）右图是杯子的侧面展开图，请在杯沿CD上确定一点P,使蚂蚁沿A-P-B路线爬行，距离最短。
（2）结合右图，求出蚂蚁爬行的最短路径长。
【答案】（1）作图见解析；（2）20cm.
【解析】（1）作出点A关于CD的对称点A1，连接A1B，交CD于点P，P为所求的点；
（2）过点B作BE⊥AC于点E，利用轴对称的性质和勾股定理可求得线段A1B的长，就是蚂蚁爬行的最短路径长.
试题解析：
（1）如图，作点A关于CD的对称点A1，连接A1B交CD于点P，点P为所求点；
(2)过点B作BE垂直AC于E，
∵点A1、A关于CD对称，
∴A1C=AC=2cm，PA1=PA，
∴PA+PB=PA1+PB=A1B，
∵在Rt△A1EB中，A1B=
（cm），
∴蚂蚁爬行的最短距离是20cm.
练习册系列答案
相关题目
