题目内容
【题目】如图,在△ABC中,AB=AC,AD是BC边上的高,点E、F是AD的三等分点,若△ABC的面积为12cm2 , 则图中阴影部分的面积是cm2 . 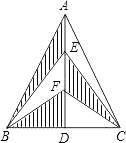
【答案】6
【解析】解:∵△ABC中,AB=AC,AD是BC边上的高,∴△ABC是轴对称图形,且直线AD是对称轴,
∴△CEF和△BEF的面积相等,
∴S阴影=S△ABD ,
∵AB=AC,AD是BC边上的高,
∴BD=CD,
∴S△ABD=S△ACD= ![]() S△ABC ,
S△ABC ,
∵S△ABC=12cm2 ,
∴S阴影=12÷2=6cm2 .
所以答案是:6.
【考点精析】通过灵活运用等腰三角形的性质和轴对称的性质,掌握等腰三角形的两个底角相等(简称:等边对等角);关于某条直线对称的两个图形是全等形;如果两个图形关于某直线对称,那么对称轴是对应点连线的垂直平分线;两个图形关于某直线对称,如果它们的对应线段或延长线相交,那么交点在对称轴上即可以解答此题.

练习册系列答案
相关题目