题目内容
【题目】在△ABC中,AB=AC.
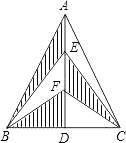
(1)如图1,如果∠BAD=30°,AD是BC上的高,AD=AE,则∠EDC= 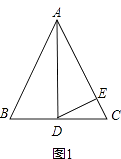
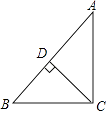
(2)如图2,如果∠BAD=40°,AD是BC上的高,AD=AE,则∠EDC= 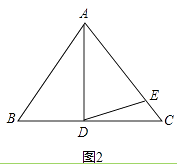
(3)思考:通过以上两题,你发现∠BAD与∠EDC之间有什么关系?请用式子表示:
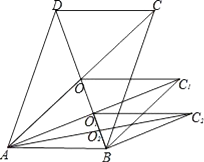
(4)如图3,如果AD不是BC上的高,AD=AE,是否仍有上述关系?如有,请你写出来,并说明理由. 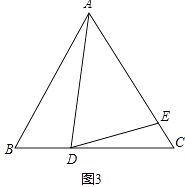
【答案】
(1)15°
(2)20°
(3)∠EDC= ![]() ∠BA
∠BA
(4)解:仍成立,理由如下
∵AD=AE,∴∠ADE=∠AED,
∴∠BAD+∠B=∠ADC=∠ADE+∠EDC=∠AED+∠EDC=(∠EDC+∠C)+∠EDC
=2∠EDC+∠C
又∵AB=AC,
∴∠B=∠C
∴∠BAD=2∠EDC
【解析】解:(1)∵在△ABC中,AB=AC,AD是BC上的高,
∴∠BAD=∠CAD,
∵∠BAD=30°,
∴∠BAD=∠CAD=30°,
∵AD=AE,
∴∠ADE=∠AED=75°,
∴∠EDC=15°.(2)∵在△ABC中,AB=AC,AD是BC上的高,
∴∠BAD=∠CAD,
∵∠BAD=40°,
∴∠BAD=∠CAD=40°,
∵AD=AE,
∴∠ADE=∠AED=70°,
∴∠EDC=20°.(3)∠BAD=2∠EDC(或∠EDC= ![]() ∠BAD)
∠BAD)
【考点精析】本题主要考查了等腰三角形的性质的相关知识点,需要掌握等腰三角形的两个底角相等(简称:等边对等角)才能正确解答此题.

 品学双优卷系列答案
品学双优卷系列答案 小学期末冲刺100分系列答案
小学期末冲刺100分系列答案 期末复习检测系列答案
期末复习检测系列答案 超能学典单元期中期末专题冲刺100分系列答案
超能学典单元期中期末专题冲刺100分系列答案 黄冈360度定制密卷系列答案
黄冈360度定制密卷系列答案【题目】某学校将为初一学生开设ABCDEF共6门选修课,现选取若干学生进行了“我最喜欢的一门选修课”调查,将调查结果绘制成如图统计图表(不完整)
选修课 | A | B | C | D | E | F |
人数 | 40 | 60 | 100 |
根据图表提供的信息,下列结论错误的是( )
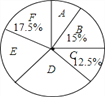
A. 这次被调查的学生人数为400人
B. 扇形统计图中E部分扇形的圆心角为72°
C. 被调查的学生中喜欢选修课E、F的人数分别为80,70
D. 喜欢选修课C的人数最少