Question

要用圆形铁片截出边长为2的正方形铁片，选用的圆形铁片的半径至少是

 

．

Answer 1

分析：该题的实质是求出正方形外接圆的半径a，我们知道，正方形内接圆的圆心为其对角线的交点，其半径就是正方形对角线的一半，故其选用的圆形铁片的最小半径为其内接圆的半径，即

2 a

2

．

解答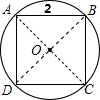：解：如图，四边形ABCD是正方形，⊙O是正方形ABCD的外接圆，AB=2，
∴AC⊥BD，A0=BO，
∴△AOB是等腰直角三角形，
∴⊙O的半径AO=

2

2

×AB=

2

2

×2=

2

；
∴选用的圆形铁片的半径至少是

2

．
故答案是：

2

．

点评：本题考查了正方形的性质．正方形的外接圆圆心是其对角线的交点，正方形的两对角线互相垂直、平分．