题目内容
 将矩形纸片ABCD按如图所示的方式折叠,AE、EF为折痕,∠BAE=30°,BE=
将矩形纸片ABCD按如图所示的方式折叠,AE、EF为折痕,∠BAE=30°,BE=| 3 |
A、3
| ||
| B、3 | ||
C、4
| ||
| D、4 |
分析:首先由折叠的性质,可得:∠AEB=∠AEC1,EC=EC1,然后由四边形ABCD是矩形,易求得∠AEC1=∠AEB=60°,即可证得△AEC1是等边三角形,可得AE=EC,又由直角三角形的性质,求得AE的长,则问题得解.
解答:解:由题意得:∠AEB=∠AEC1,EC=EC1,
∵四边形ABCD是矩形,
∴AD∥BC,∠B=90°,
∵∠BAE=30°,
∴∠AEB=60°,
∴∠DAE=∠AEB=60°,
∴∠AEC1=∠AEB=60°,
∴△AEC1是等边三角形,
∴AE=EC1,
∴在Rt△ABE中,∠BAE=30°,BE=
,
∴AE=2BE=2
,
∴EC=2
,
∴BC=AE+EC=3
.
故选A.
∵四边形ABCD是矩形,
∴AD∥BC,∠B=90°,
∵∠BAE=30°,
∴∠AEB=60°,
∴∠DAE=∠AEB=60°,
∴∠AEC1=∠AEB=60°,
∴△AEC1是等边三角形,
∴AE=EC1,
∴在Rt△ABE中,∠BAE=30°,BE=
| 3 |
∴AE=2BE=2
| 3 |
∴EC=2
| 3 |
∴BC=AE+EC=3
| 3 |
故选A.
点评:此题考查了折叠的性质,矩形的性质,等边三角形的判定与性质以及直角三角形的性质等知识.此题综合性较强,难度适中,解题的关键是注意数形结合思想的应用.

练习册系列答案
 开心练习课课练与单元检测系列答案
开心练习课课练与单元检测系列答案 开心试卷期末冲刺100分系列答案
开心试卷期末冲刺100分系列答案
相关题目
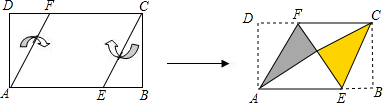
将矩形纸片ABCD按如图所示的方式折叠,得到菱形AECF.若AB=3,则BC的长为( )

| A、1 | ||
| B、2 | ||
C、
| ||
D、
|
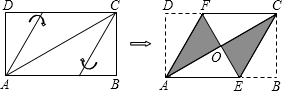 C的长为
C的长为

