题目内容
【题目】某数学活动小组在一次活动中,对一个数学问题作如下探究:
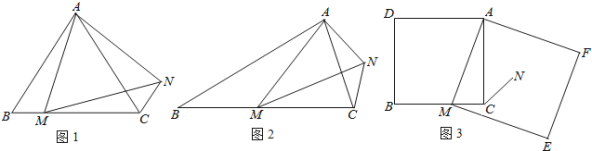
问题发现:如图1,在等边三角形ABC中,点M是边BC上任意一点,连接AM,以AM为边作等边三角形AMN,连接CN,证明:BM=CN.
变式探究:如图2,在等腰三角形ABC中,BA=BC,∠ABC=∠α,点M为边BC上任意一点,以AM为腰作等腰三角形AMN,MA=MN,使∠AMN=∠ABC,连接CN,请求出![]() 的值.(用含α的式子表示出来)
的值.(用含α的式子表示出来)
解决问题:如图3,在正方形ADBC中,点M为边BC上一点,以AM为边作正方形作AMEF,N为正方形AMEF的中心,连接CN,若正方形AMEF的边长为![]() ,CN=
,CN=![]() ,请你求正方形ADBC的边长.
,请你求正方形ADBC的边长.
【答案】问题发现:证明见解析;变式探究:2sin![]() ;解决问题:3
;解决问题:3
【解析】
试题分析:问题发现:根据△ABC,△AMN为等边三角形,得到AB=AC,AM=AN且∠BAC=∠MAN=60°从而得到∠BAC﹣∠CAM=∠MAN﹣∠CAM,即∠BAM=∠CAN,证明△BAM≌△CAN,即可得到BM=CN.
变式探究:根据△ABC,△AMN为等腰三角形,得到![]() =1且∠ABC=∠AMN,证明△ABC~△AMN,得到
=1且∠ABC=∠AMN,证明△ABC~△AMN,得到![]() ,利用等腰三角形的性质BA=BC,得到
,利用等腰三角形的性质BA=BC,得到![]() ,
,![]() ,证明△ABM~△ACN,得到
,证明△ABM~△ACN,得到![]() ,作BD⊥AC,如图2,再由AB=BC,得到∠ABD=
,作BD⊥AC,如图2,再由AB=BC,得到∠ABD=![]() ,根据sin∠ABD=
,根据sin∠ABD=![]() ,得到AD=ABsin
,得到AD=ABsin![]() ,则AC=2AD=2ABsin
,则AC=2AD=2ABsin![]() ,从而得到
,从而得到![]() =2sin
=2sin![]() .
.
解决问题:利用四边形ADBC,AMEF为正方形,得到∠ABC=∠BAC=45°∠MAN=45°,即∠BAM=∠CAN,由![]() ,得到
,得到![]() ,证明△ABM~△ACN,得到
,证明△ABM~△ACN,得到![]() ,进而得到
,进而得到![]() =cos45°=
=cos45°=![]() ,求出BM=2,设AC=x,利用勾股定理,在Rt△AMC,AC2+CM2=AM2,即x2+(x﹣2)2=10,解得:x1=3,x2=﹣1(舍去),即可解答.
,求出BM=2,设AC=x,利用勾股定理,在Rt△AMC,AC2+CM2=AM2,即x2+(x﹣2)2=10,解得:x1=3,x2=﹣1(舍去),即可解答.
解:问题发现,
∵△ABC,△AMN为等边三角形,
∴AB=AC,AM=AN且∠BAC=∠MAN=60°
∴∠BAC﹣∠CAM=∠MAN﹣∠CAM,
∴∠BAM=∠CAN,
在△BAM与△CAN中,
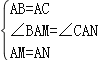 ,
,
∴△BAM≌△CAN,
∴BM=CN.
变式探究:∵![]() =1且∠ABC=∠AMN,
=1且∠ABC=∠AMN,
∴△ABC~△AMN,
∴![]() ,
,
∵AB=BC,
∴![]() ,
,
∵AM=MN
∴![]() ,
,
∴∠BAM=∠CAN,
∴△ABM~△ACN,
∴![]() ,
,
作BD⊥AC,如图2,

∵AB=BC,
∴∠ABD=![]() ,
,
∴sin∠ABD=![]() ,
,
∴AD=ABsin![]()
∴AC=2AD=2ABsin![]() ,
,
∴![]() =2sin
=2sin![]()
解决问题:
如图3,连接AB,AN.
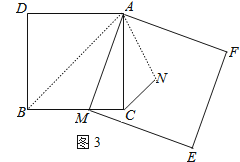
∵四边形ADBC,AMEF为正方形,
∴∠ABC=∠BAC=45°∠MAN=45°,
∴∠BAC﹣∠MAC=∠MAN﹣∠MAC
即∠BAM=∠CAN,
∵![]() ,
,
∴![]() ,
,
∴△ABM~△ACN,
∴![]()
∴![]() =cos45°=
=cos45°=![]() ,
,
∴![]()
∴BM=2,
设AC=x,
在Rt△AMC,
AC2+CM2=AM2
即x2+(x﹣2)2=10,
解得:x1=3,x2=﹣1(舍去),
答:边长为3.

【题目】 (2016新疆生产建设兵团第6题)某小组同学在一周内参加家务劳动时间与人数情况如表所示:
劳动时间(小时) | 2 | 3 | 4 |
人数 | 3 | 2 | 1 |
下列关于“劳动时间”这组数据叙述正确的是( )
A.中位数是2 B.众数是2 C.平均数是3 D.方差是0


