题目内容
【题目】如图,矩形ABCD中,BC=2AB=4,AE平分∠BAD交边BC于点E,∠AEC的分线交AD于点F,以点D为圆心,DF为半径画圆弧交边CD于点G,求FG的长.
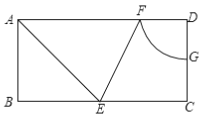
【答案】![]()
【解析】试题分析:先由矩形的性质得出,∠BAD=∠B=∠D=90°,AD=BC=4,AD∥BC,根据AE平分∠BAD得到∠BAE=∠EAD=45°,那么△ABE是等腰直角三角形,于是AB=BE=2,AE=![]() AB=2
AB=2![]() .再由∠AEC的分线交AD于点F,∠AEF=∠CEF,由AD∥BC,得出∠CEF=∠AFE,等量代换得到∠AEF=∠AFE,那么AF=AE=2
.再由∠AEC的分线交AD于点F,∠AEF=∠CEF,由AD∥BC,得出∠CEF=∠AFE,等量代换得到∠AEF=∠AFE,那么AF=AE=2![]() ,DF=AD-AF=4-2
,DF=AD-AF=4-2![]() ,然后根据弧长的计算公式即可求出
,然后根据弧长的计算公式即可求出![]() 的长.
的长.
试题解析:∵四边形ABCD是矩形,
∴∠BAD=∠B=∠D=90°,AD=BC=4,AD∥BC,
∵AE平分∠BAD交边BC于点E,
∴∠BAE=∠EAD=45°,
∴△ABE是等腰直角三角形,
∴AB=BE=2,AE=![]() AB=2
AB=2![]()
∵∠AEC的分线交AD于点F,
∴∠AEF=∠CEF,
∵AD∥BC,
∴∠CEF=∠AFE,
∴∠AEF=∠AFE,
∴AF=AE=2![]()
∴DF=AD-AF=4-2![]()
∴![]() 的长为:
的长为: 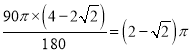 .
.

练习册系列答案
相关题目