题目内容
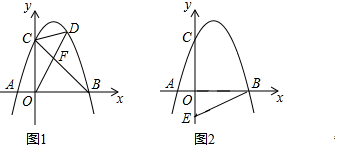
【题目】已知,二次函数![]() (m,n为常数且m≠0)
(m,n为常数且m≠0)
(1)若n=0,请判断该函数的图像与x轴的交点个数,并说明理由;
(2)若点A(n+5,n)在该函数图像上,试探索m,n满足的条件;
(3)若点(2,p),(3,q),(4,r)均在该函数图像上,且p<q<r,求m的取值范围.
【答案】(1) 函数图像与![]() 轴有两个交点; (2)
轴有两个交点; (2) ![]() 或
或![]() ; (3)
; (3) ![]() 且m≠0
且m≠0
【解析】
(1)先确定△=b2-4ac>0,可得函数图象与![]() 轴有两个交点;(2)将点A代入
轴有两个交点;(2)将点A代入![]() 中即可得m,n应满足的关系;(3)根据二次函数的增减性进行分类讨论.
中即可得m,n应满足的关系;(3)根据二次函数的增减性进行分类讨论.
解: (1)当![]() 时,原函数为
时,原函数为![]()
![]()
![]()
![]()
![]() 该函数图像与
该函数图像与![]() 轴有两个交点
轴有两个交点
(2)将![]() 代入原函数得:
代入原函数得:![]()
![]()
![]() 或
或![]()
(3) 对称轴![]()
①当2,3,4在对称轴的同一侧时,![]() 且m≠0
且m≠0
![]() 且m≠0
且m≠0
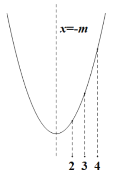
②当2,3,4在对称轴两侧时,![]()
![]()
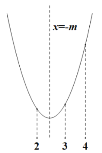
综上:![]() 且m≠0
且m≠0

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
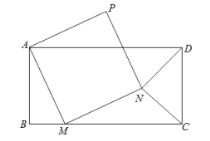
【题目】如图,已知矩形![]() ,点
,点![]() 为线段
为线段![]() 上一动点,沿线段
上一动点,沿线段![]() 由
由![]() 向
向![]() 运动,连接
运动,连接![]() ,以
,以![]() 为边向右侧作正方形
为边向右侧作正方形![]() ,连接
,连接![]() ,设
,设![]() 的路程即
的路程即![]() 的长为
的长为![]() ,
,![]() 间的距离为
间的距离为![]() ,
,![]() 间的距离为
间的距离为![]() .
.
数学兴趣小组的小刚根据学习函数的经验,分别对函数![]() 随自变量
随自变量![]() 的变化而变化的规律进行探究,过程如下:
的变化而变化的规律进行探究,过程如下:
(1)根据下表中自变量![]() 的取值进行去电,画图,测量,分别得到几组对应值,请将表格补充完成.
的取值进行去电,画图,测量,分别得到几组对应值,请将表格补充完成.
| 0 | 1 | 2 | 3 | 4 | 5 | 6 |
| 3 | 2.22 |
| 3 | 4.11 | 5.39 | 6.72 |
| 4.24 | 2.81 | 1.39 | 0 |
| 2.84 | 4.26 |
其中,![]() ,
,![]() ;
;
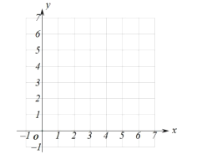
(2)在同一平面黄子佼坐标系中,描点![]() ,并画出
,并画出![]() 的函数图像;
的函数图像;
(3)当![]() 为等腰三角形时,
为等腰三角形时,![]() 的长度约为 .
的长度约为 .