Question

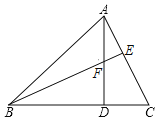
【题目】已知锐角△ABC，∠ABC＝45°，AD⊥BC于D，BE⊥AC于E，交AD于F．

（1）求证：△BDF≌△ADC；

（2）若BD＝4，DC＝3，求线段BE的长度．

Answer 1

【答案】（1）见解析；（2）BE＝.

【解析】

（1）由题意可得AD=BD，由余角的性质可得∠CBE=∠DAC，由“ASA”可证△BDF≌△ADC；（2）由全等三角形的性质可得AD=BD=4，CD=DF=3，BF=AC，由三角形的面积公式可求BE的长度.

解：（1）∵AD⊥BC，∠ABC＝45°

∴∠ABC＝∠BAD＝45°，

∴AD＝BD，

∵DA⊥BC，BE⊥AC

∴∠C+∠DAC＝90°，∠C+∠CBE＝90°

∴∠CBE＝∠DAC，且AD＝BD，∠ADC＝∠ADB＝90°

∴△BDF≌△ADC（ASA）

（2）∵△BDF≌△ADC

∴AD＝BD＝4，CD＝DF＝3，BF＝AC

∴BF＝ ＝5

∴AC＝5，

∵S△ABC＝×BC×AD＝×AC×BE

∴7×4＝5×BE

∴BE＝.