题目内容
【题目】如图,在△ABC中,AD是BC边上的中线,点E、F在AB边上,且E是BF中点,连接DE,CF交AD于G,。
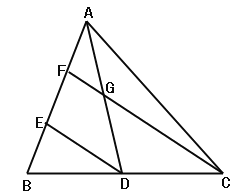
(1)求证:△AFG∽△AED
(2)若FG=3,G为AD中点,求CG的长
【答案】(1)证明见解析;(2)9.
【解析】
试题分析:(1)根据AD是BC边上的中线,点E是BF中点,得到BD=CD,BE=EF,根据三角形的中位线的性质得到DE∥CF,即可得到结论;
(2)由G为AD中点,FG∥DE,得到AF=EF,求得DE=2FG=6,根据三角形的中位线的性质得到CF=2DE=8,即可得到结论.
试题解析:(1)∵AD是BC边上的中线,点E是BF中点,
∴BD=CD,BE=EF,
∴DE是△BCF的中位线,
∴DE∥CF,
∴DE∥FG,
∴△AFG∽△AED;
(2)∵G为AD中点,FG∥DE,
∴AF=EF,
∴FG是△ADE的中位线,
∴DE=2FG=6,
∴CF=2DE=12,
∴CG=FC-FG=12-3=9.

练习册系列答案
相关题目