题目内容
已知，如图，AD∥BC，∠1=∠2，∠A=120°，且BD⊥CD，求∠C的度数．
解：∵AD∥BC，
∴∠ABC=180°-∠A=60°，∠ADB=∠2，
∵∠1=∠2，
∴∠1=∠ADB=∠2=30°，
∵BD⊥CD，
∴∠BDC=90°，
∠C=180°-（30°+90°）=60°，
故∠C的度数为60°．
分析：根据平行线的性质先求出∠ADB=∠2=30°，再根据垂直定义及平行线性质即可求出∠C的度数．
点评：本题主要考查平行线的性质：两直线平行，内错角相等，同旁内角互补．
∴∠ABC=180°-∠A=60°，∠ADB=∠2，
∵∠1=∠2，
∴∠1=∠ADB=∠2=30°，
∵BD⊥CD，
∴∠BDC=90°，
∠C=180°-（30°+90°）=60°，
故∠C的度数为60°．
分析：根据平行线的性质先求出∠ADB=∠2=30°，再根据垂直定义及平行线性质即可求出∠C的度数．
点评：本题主要考查平行线的性质：两直线平行，内错角相等，同旁内角互补．
练习册系列答案
相关题目
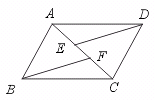27、已知：如图，AD∥BC，ED∥BF，且AF=CE．
25、已知，如图，AD∥BC，∠1=∠2，∠A=120°，且BD⊥CD，求∠C的度数．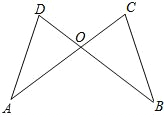
已知：如图，AD=BC，AC=BD．试判断OD、OC的数量关系，并说明理由．
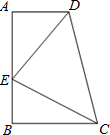已知，如图，AD∥BC，∠A=90°，AD=BE，∠EDC=∠ECD，请你说明下列结论成立的理由：（1）△AED≌△BCE，（2）AB=AD+BC．
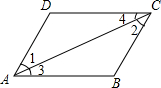根据题意填空：