题目内容
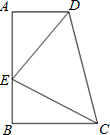 已知,如图,AD∥BC,∠A=90°,AD=BE,∠EDC=∠ECD,请你说明下列结论成立的理由:(1)△AED≌△BCE,(2)AB=AD+BC.
已知,如图,AD∥BC,∠A=90°,AD=BE,∠EDC=∠ECD,请你说明下列结论成立的理由:(1)△AED≌△BCE,(2)AB=AD+BC.
分析:(1)由AD∥BC,∠A=90°,根据两直线平行,同旁内角互补,可得∠B=90°,根据直角三角形的HL定理,即可证得;
(2)由(1)△AED≌△BCE,根据全等三角形的性质,可得AE=BC,又AB=AE+BE,等量代换,即可得出;
(2)由(1)△AED≌△BCE,根据全等三角形的性质,可得AE=BC,又AB=AE+BE,等量代换,即可得出;
解答:证明:(1)∵AD∥BC,∠A=90°,
∴∠B=90°,
∵∠EDC=∠ECD,
∴ED=EC,
在直角△AED和直角△BCE中,
,
∴△AED≌△BCE;
(2)∵△AED≌△BCE,
∴AE=BC,AD=BE,
又∵AB=AE+BE,
∴AB=AD+BC.
∴∠B=90°,
∵∠EDC=∠ECD,
∴ED=EC,
在直角△AED和直角△BCE中,
|
∴△AED≌△BCE;
(2)∵△AED≌△BCE,
∴AE=BC,AD=BE,
又∵AB=AE+BE,
∴AB=AD+BC.
点评:本题主要考查了全等三角形的判定与性质,全等三角形的判定是结合全等三角形的性质证明线段和角相等的重要工具,在判定三角形全等时,关键是选择恰当的判定条件.

练习册系列答案
 新课标快乐提优暑假作业陕西旅游出版社系列答案
新课标快乐提优暑假作业陕西旅游出版社系列答案 暑假衔接培优教材浙江工商大学出版社系列答案
暑假衔接培优教材浙江工商大学出版社系列答案
相关题目
 27、已知:如图,AD∥BC,ED∥BF,且AF=CE.
27、已知:如图,AD∥BC,ED∥BF,且AF=CE. 25、已知,如图,AD∥BC,∠1=∠2,∠A=120°,且BD⊥CD,求∠C的度数.
25、已知,如图,AD∥BC,∠1=∠2,∠A=120°,且BD⊥CD,求∠C的度数.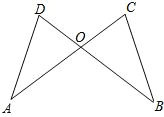 已知:如图,AD=BC,AC=BD.试判断OD、OC的数量关系,并说明理由.
已知:如图,AD=BC,AC=BD.试判断OD、OC的数量关系,并说明理由. 根据题意填空:
根据题意填空: