题目内容
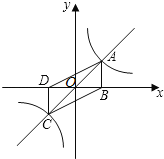
【题目】如图,正比例函数y=x与反比例函数y=![]() 的图象相交于A,C两点,AB⊥x轴于B,CD⊥x轴于D,则四边形ABCD的面积为 .
的图象相交于A,C两点,AB⊥x轴于B,CD⊥x轴于D,则四边形ABCD的面积为 .
【答案】2
【解析】
试题分析:首先根据反比例函数图象上的点与原点所连的线段、坐标轴、向坐标轴作垂线所围成的直角三角形面积S的关系即S=![]() |k|,得出S△AOB=S△ODC=
|k|,得出S△AOB=S△ODC=![]() ,再根据反比例函数的对称性可知:OB=OD,得出S△ADB+S△BDC得出结果.
,再根据反比例函数的对称性可知:OB=OD,得出S△ADB+S△BDC得出结果.
解:根据反比例函数的对称性可知:OB=OD,AB=CD,
∵四边形ABCD的面积等于S△ADB+S△BDC,
∵A(1,1),B(1,0),C(﹣1,﹣1),D(﹣1,0)
∴S△ADB=![]() (DO+OB)×AB=
(DO+OB)×AB=![]() ×2×1=1,
×2×1=1,
S△BDC=![]() (DO+OB)×DC=
(DO+OB)×DC=![]() ×2×1=1,
×2×1=1,
∴四边形ABCD的面积=2.
故答案为:2.

练习册系列答案
 开心快乐假期作业暑假作业西安出版社系列答案
开心快乐假期作业暑假作业西安出版社系列答案 名题训练系列答案
名题训练系列答案
相关题目
【题目】抛物线y=ax2+bx+c(a≠0)上部分点的横坐标x,纵坐标y的对应值如表:
x | … | ﹣1 | 0 | 1 | 2 | 3 | 4 | … |
y | … | ﹣ | 1 |
| 3 |
| 1 | … |
从上表可知,下列说法错误的是( )
A.对称轴为直线x=2
B.图象开口向下
C.顶点坐标(2,3)
D.当x=5时,y=![]()