题目内容
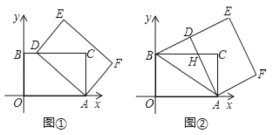
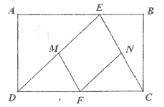
【题目】如图,四边形![]() 是矩形,点
是矩形,点![]() 是边
是边![]() 上一个动点,点
上一个动点,点![]() ,
,![]() ,
,![]() 是
是![]() ,
,![]() ,
,![]() 的中点.
的中点.
(1)求证:![]() ;
;
(2)若四边形![]() 是正方形,求
是正方形,求![]() 的值.
的值.
【答案】(1)证明见解析;(2)![]() .
.
【解析】
(1)由三角形中位线定理可得DM=EM=FN,MF=EN=CN,DF=CF,由“SSS”可证△DMF≌△FNC; (2)由正方形的性质可得EN=NF=EM=MF,NE⊥EM,可得DE=EC,可得∠EDC=∠ECD=45°,可证AD=AE,BC=BE,即可求AD:AB的值.
证明:(1)∵点F,M,N分别是DC,DE,CE的中点.
∴DM=EM=FN,MF=EN=CN,DF=CF
∴△DMF≌△FNC(SSS)
(2)∵四边形MENF是正方形.
∴EN=NF=EM=MF,NE⊥EM,
∴DE=EC ∴∠EDC=∠ECD=45°,
∵AB∥CD
∴∠AED=∠EDC=45°,∠BEC=∠ECD=45°
∴∠A=∠B=90° ∴∠AED=∠ADE=45°,
∠BEC=∠BCE=45°
∴AD=AE,BC=BE,
∴AB=AE+BE=2AD
∴AD:AB=1:2.

练习册系列答案
相关题目