题目内容
如图，在Rt△ABC中，∠C=90°．
（1）按要求用尺规作图：作BE平分∠ABC交AC于点E；过点E作ED⊥BE交AB于点D；作△BDE的外接圆；
（2）判断直线AC与△BDE外接圆的位置关系，并说明理由．
（1）按要求用尺规作图：作BE平分∠ABC交AC于点E；过点E作ED⊥BE交AB于点D；作△BDE的外接圆；
（2）判断直线AC与△BDE外接圆的位置关系，并说明理由．
（1）如图1所示：
（2）证明：如图2所示：
连接OE，
∵BE平分∠ABC交AC于点E，
∴∠1=∠2，
∵BO=OE，
∴∠1=∠4，
∴∠2=∠4，
∵∠2+∠3=90°，
∴∠3+∠4=90°，
∴直线AC与△BDE外接圆相切．
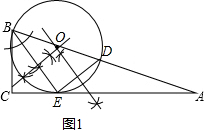
（2）证明：如图2所示：
连接OE，
∵BE平分∠ABC交AC于点E，
∴∠1=∠2，
∵BO=OE，∴∠1=∠4，
∴∠2=∠4，
∵∠2+∠3=90°，
∴∠3+∠4=90°，
∴直线AC与△BDE外接圆相切．
练习册系列答案
相关题目
