Question

【题目】平面直角坐标系中，横坐标为2的点A在反比例函数y(k＞0)的图象上，过点A作AB⊥x轴于点B，．

(1)求k的值；

(2)在x轴的负半轴上找点P，将点A绕点P顺时针旋转90°，其对应点A落在此反比例函数第三象限的图象上，求点P的坐标；

(3)直线yx+n(n＜0)与AB的延长线交于点C，与反比例函数图象交于点E，若点E到直线AB的距离等于AC，求n的值．

Answer 1

【答案】(1)k=8；(2)点P坐标为(﹣1，0)；(3)n的值为﹣3或．

【解析】

（1）设OAa，则AB＝2a，OB＝2，利用勾股定理解出a，得到A点，代入得到k即可；（2）过点A′作AG⊥x轴交于点G，设点P(a，0)，易证△PAB≌△A′PG，得到点A′的坐标为(a+4，a﹣2)，得(a+4)(a﹣2)＝8，解出a即可；（3）设线yx+n(n＜0)与AB和双曲线分别交于点C、点E(E′)，过点E(E′)作E(′E)F(F′)⊥AB交于点F(F′)，E点有两种情况，在第一象限或者第三象限，将直线表达式与反比例函数表达式联立，用n表示出EF，E到直线AB的距离为FE等于AC，得到方程解出n即可

解：(1)，设：OAa，则AB＝2a，OB＝2，

由勾股定理得：(a)2＝(2a)2+4，解得：a＝2，

则点A(2，4)，

则k＝2×4＝8；

(2)点A绕点P顺时针旋转90°，点A对应点A′落在此反比例函数第三象限的图象上，

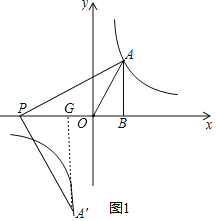
过点A′作AG⊥x轴交于点G，设点P(a，0)，

∵∠PAB+∠BPA＝90°，∠BPA+∠A′PG＝90°，

∴∠A′PG＝∠PAB，

∠ABP＝∠A′GP＝90°，PA＝PA′，

∴△PAB≌△A′PG(AAS)，

∴PG＝AB＝4，GA′＝PB＝2﹣a，

则点A′的坐标为(a+4，a﹣2)，

则(a+4)(a﹣2)＝8，

解得：a＝﹣1(正值已舍去)

故点P坐标为(﹣1，0)；

(3)设线yx+n(n＜0)与AB和双曲线分别交于点C、点E(E′)

过点E(E′)作E(′E)F(F′)⊥AB交于点F(F′)，

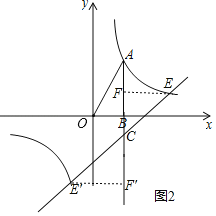
①当直线与双曲线交点为E时，

则点C(2，1+n)，AC＝4﹣1﹣n＝3﹣n，

将直线表达式与反比例函数表达式联立并整理得：x2+2nx﹣16＝0，

解得：x＝﹣n±，则xE＝﹣n，

则EF＝﹣n2，

E到直线AB的距离为FE等于AC，

则﹣n2＝3﹣n，

解得：n＝﹣3(正值已舍去)；

②当直线与双曲线交点为E′时，

同理可得：n；

故：n的值为﹣3或．