题目内容
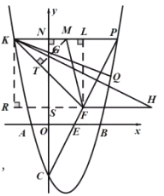
【题目】在平面直角坐标系![]() 中,抛物线
中,抛物线![]() 交
交![]() 轴于
轴于![]() ,
,![]() 两点,交
两点,交![]() 轴于点
轴于点![]() .
.
(1)如图,求抛物线的解析式;
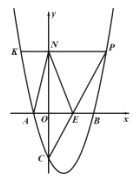
(2)如图,点![]() 是第一象限抛物线上的一个动点,连接
是第一象限抛物线上的一个动点,连接![]() 交
交![]() 轴于点
轴于点![]() ,过点
,过点![]() 作
作![]() 轴交抛物线于点
轴交抛物线于点![]() ,交
,交![]() 轴于点
轴于点![]() ,连接
,连接![]() 、
、![]() 、
、![]() ,设点
,设点![]() 的横坐标为
的横坐标为![]() ,四边形
,四边形![]() 的面积为
的面积为![]() ,求
,求![]() 与
与![]() 之间的函数关系式(不要求写出自变量
之间的函数关系式(不要求写出自变量![]() 的取值范围);
的取值范围);
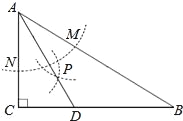
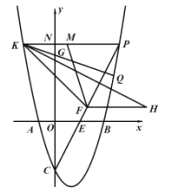
(3)如图,在(2) 的条件下,点![]() 是
是![]() 中点,过点
中点,过点![]() 作
作![]() 的垂线与过点
的垂线与过点![]() 平行于
平行于![]() 轴的直线交于点
轴的直线交于点![]() ,
, ![]() ,点
,点![]() 为第一象限内直线
为第一象限内直线![]() 下方抛物线上一点,连接
下方抛物线上一点,连接![]() 交
交![]() 轴于点
轴于点![]() ,点
,点![]() 是
是![]() 上一点,连接
上一点,连接![]() 、
、![]() ,若
,若![]() ,
,![]() ,求点
,求点![]() 坐标
坐标
【答案】(1)![]() ;(2)
;(2)![]() ;(3)
;(3)![]()
【解析】
(1)把A,B点代入解析式即可
(2)过点![]() 作
作![]() 轴,交
轴,交![]() 轴于点
轴于点![]() ,点
,点![]() ,可得
,可得![]() ,即可解答
,即可解答
(3)过点![]() 作
作![]() 于点
于点![]() ,
,![]() ,
,![]() ,求出点
,求出点![]() ,再根据对称轴
,再根据对称轴![]() ,由对称性得
,由对称性得![]() ,然后设点
,然后设点![]() 过点
过点![]() 作
作![]() 交
交![]() 于
于![]() ,得到NG,MP,KM的值,过点
,得到NG,MP,KM的值,过点![]() 作
作![]() 于点
于点![]() ,
,![]() 得到
得到![]() ,过点
,过点![]() 作
作![]() 于点
于点![]() ,
,![]() ,求出m即可解答
,求出m即可解答
(1)解![]() 抛物线
抛物线![]() 过点
过点![]() ,
,![]()
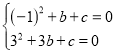 解得
解得![]()
![]() 抛物线解析式为
抛物线解析式为![]()
(2)过点![]() 作
作![]() 轴,交
轴,交![]() 轴于点
轴于点![]() ,点
,点![]() ,
,
![]() ,
,![]()
![]()
![]()
![]()
(3)过点![]() 作
作![]() 于点
于点![]() ,
,![]() ,
,![]()
![]()
![]()
![]()
![]() 点
点![]() 是
是![]() 中点
中点
![]()
![]()
![]() ,
,![]() (舍),
(舍),![]() .
.
![]() 点
点![]() ,
,
![]() ,
,
![]() 对称轴
对称轴![]() ,由对称性得
,由对称性得![]() .
.
![]() ,
,![]() ,设点
,设点![]() 过点
过点![]() 作
作![]() 交
交![]() 于
于![]() .
.
![]()
![]()
![]() ,
,![]() ,
,![]()
![]()
![]()
过点![]() 作
作![]() 于点
于点![]() ,
,![]()
![]()
![]()
![]()
![]()
过点![]() 作
作![]() 于点
于点![]() ,
,![]()
![]()
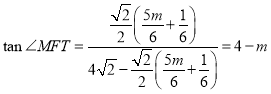
解得![]() (舍),
(舍),![]()
![]()

练习册系列答案
 口算题卡北京妇女儿童出版社系列答案
口算题卡北京妇女儿童出版社系列答案
相关题目