题目内容
矩形ABCD的周长为56，对角线AC，BD交于点O，△ABO与△BCO的周长差为4，则AB的长是
- A.12
- B.22
- C.16
- D.26
C
试题分析：根据矩形的性质可得OA=OB=OC=OD，AB=CD，AD=BC，再结合矩形ABCD的周长为56，△ABO与△BCO的周长差为4，即可求得结果.
∵矩形ABCD，
∴OA=OB=OC=OD，AB=CD，AD=BC，
∵矩形ABCD的周长为56，
∴AB+BC=28，
∵△ABO与△BCO的周长差为4，
∴（AB+BO+AO）-（BC+BO+CO）=4，即AB-BC=4，
∴AB=16，
故选C.
考点：本题考查的是矩形的性质
点评：解答本题的关键是熟记矩形的对边相等，对角线互相平分且相等.
试题分析：根据矩形的性质可得OA=OB=OC=OD，AB=CD，AD=BC，再结合矩形ABCD的周长为56，△ABO与△BCO的周长差为4，即可求得结果.
∵矩形ABCD，
∴OA=OB=OC=OD，AB=CD，AD=BC，
∵矩形ABCD的周长为56，
∴AB+BC=28，
∵△ABO与△BCO的周长差为4，
∴（AB+BO+AO）-（BC+BO+CO）=4，即AB-BC=4，
∴AB=16，
故选C.
考点：本题考查的是矩形的性质
点评：解答本题的关键是熟记矩形的对边相等，对角线互相平分且相等.
练习册系列答案
小学教材全测系列答案
相关题目
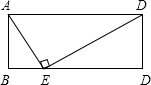如图，在矩形ABCD中，E是BC上一点且∠AED=90°，∠BAE=30°，AE=4，则矩形ABCD的周长为（ ）A、8+2
| ||
B、16+2
| ||
C、8+4
| ||
D、16+4
|
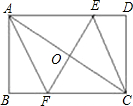CE、EF，且EF与AC相交于点O．