题目内容
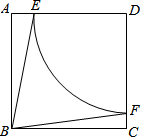 如图,以正方形ABCD的顶点D为圆心画圆,分别交AD、CD两边于点E、F,若∠ABE=15°,BE=2,则扇形DEF的面积是
如图,以正方形ABCD的顶点D为圆心画圆,分别交AD、CD两边于点E、F,若∠ABE=15°,BE=2,则扇形DEF的面积是| π |
| 2 |
| π |
| 2 |
分析:如图,连接EF.根据正方形的对称性得到∠EBF=60°,则然后由等腰直角的性质求得DE=
;最后根据扇形面积公式求解.
| 2 |
解答:
解:如图,连接EF.
∵四边形ABCD是正方形,∠ABE=15°,BE=2,
∴根据正方形的对称性得到∠ABE=∠CBF=15°,BE=BF,AE=CF,
∴∠EBF=60°,
∴△BEF是等边三角形,
∴EF=BE=2.
在等腰直角△DEF中,EF=
ED=2,则ED=
,
∴S扇形DEF=
=
.
故答案是:
.

| π |
| 2 |
∵四边形ABCD是正方形,∠ABE=15°,BE=2,
∴根据正方形的对称性得到∠ABE=∠CBF=15°,BE=BF,AE=CF,
∴∠EBF=60°,
∴△BEF是等边三角形,
∴EF=BE=2.
在等腰直角△DEF中,EF=
| 2 |
| 2 |
∴S扇形DEF=
90π×(
| ||
| 360 |
| π |
| 2 |
故答案是:
| π |
| 2 |
点评:本题考查了扇形面积的计算,等腰直角三角形,正方形的性质.求得ED的长度是解题的难点.

练习册系列答案
相关题目
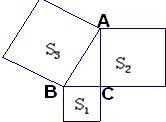 13、如图,以直角△ABC的三边向外作正方形,其面积分别为S1,S2,S3且S1=4,S2=8,则S3=
13、如图,以直角△ABC的三边向外作正方形,其面积分别为S1,S2,S3且S1=4,S2=8,则S3=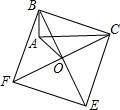 如图,以Rt△ABC的斜边BC为一边在△ABC的同侧作正方形BCEF,设正方形的中心为O,连接AO,如果AB=4,AO=6
如图,以Rt△ABC的斜边BC为一边在△ABC的同侧作正方形BCEF,设正方形的中心为O,连接AO,如果AB=4,AO=6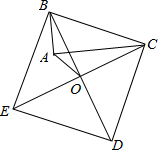 如图,以Rt△ABC的斜边BC为一边作正方形BCDE,设正方形的中心为O,连接AO,如果AB=3,AO=
如图,以Rt△ABC的斜边BC为一边作正方形BCDE,设正方形的中心为O,连接AO,如果AB=3,AO=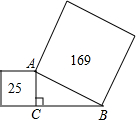 如图,以Rt△ABC的斜边和一直角边为边长向外作正方形,面积分别为169和25,则另一直角边的长度BC为( )
如图,以Rt△ABC的斜边和一直角边为边长向外作正方形,面积分别为169和25,则另一直角边的长度BC为( )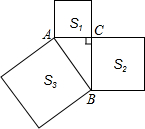 如图,以Rt△ABC各边为边长的正方形面积分别为S1、S2、S3,且S1+S2+S3=50,则AB=( )
如图,以Rt△ABC各边为边长的正方形面积分别为S1、S2、S3,且S1+S2+S3=50,则AB=( )