题目内容
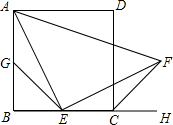 (2013•枣阳市模拟)如图,四边形ABCD是边长为a的正方形,点G,E分别是边AB,BC的中点,∠AEF=90°,且EF交正方形外角的平分线CF于点F.
(2013•枣阳市模拟)如图,四边形ABCD是边长为a的正方形,点G,E分别是边AB,BC的中点,∠AEF=90°,且EF交正方形外角的平分线CF于点F.(1)证明:∠BAE=∠FEC;
(2)求△AEF的面积.
分析:(1)由于四边形ABCD是正方形,可得∠B=90°,AB=BC,而G、E是AB、BC中点,易证BG=BE,可求∠BGE=∠BEG=45°,利用三角形外角性质可得∠BGE=∠1+∠2=45°,又知∠AEF=90°,易求∠1+∠4=45°,从而可证∠BAE=∠FEC;
(2)由(1)知∠BGE=45°,可求∠AGE=135°,而CF是外角平分线,可求∠FCE=45°,进而可求∠ECF=135°,那么∠AGE=∠ECF,根据正方形的性质以及重点定义,易证AG=EC,又知∠4=∠2,利用ASA可证△AGE≌△ECF,于是EA=EF,在Rt△ABE中利用勾股定理可求AE2=
a2,进而可求△AEF的面积.
(2)由(1)知∠BGE=45°,可求∠AGE=135°,而CF是外角平分线,可求∠FCE=45°,进而可求∠ECF=135°,那么∠AGE=∠ECF,根据正方形的性质以及重点定义,易证AG=EC,又知∠4=∠2,利用ASA可证△AGE≌△ECF,于是EA=EF,在Rt△ABE中利用勾股定理可求AE2=
| 5 |
| 4 |
解答: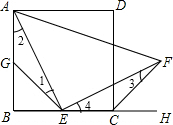 证明:如右图,
证明:如右图,
(1)∵四边形ABCD是正方形,
∴∠B=90°,AB=BC,
∵G、E是AB、BC中点,
∴BG=
AB,BE=
BC,
∴BG=BE,
∴∠BGE=∠BEG=45°,
∴∠BGE=∠1+∠2=45°,
∵∠AEF=90°,
∴∠1+∠4=180°-45°-90°=45°,
∴∠2=∠4,
即∠BAE=∠FEC;
(2)由(1)知∠BGE=45°,
∴∠AGE=135°,
∵CF是∠DCH的角平分线,
∴∠FCH=
×90°=45°,
∴∠ECF=135°,
∵四边形ABCD是正方形,
∴AB=BC,
∵G、E是AB、BC中点,
∴AG=
AB,EC=
BC,
∴AG=EC,
在△AGE和△ECF中,
,
∴△AGE≌△ECF,
∴AE=EF,
在Rt△ABE中,∵AE2=AB2+BE2,
∴AE2=
a2,
∴S△AEF=
×AE×EF=
AE2=
×
a2=
a2.
 证明:如右图,
证明:如右图,(1)∵四边形ABCD是正方形,
∴∠B=90°,AB=BC,
∵G、E是AB、BC中点,
∴BG=
| 1 |
| 2 |
| 1 |
| 2 |
∴BG=BE,
∴∠BGE=∠BEG=45°,
∴∠BGE=∠1+∠2=45°,
∵∠AEF=90°,
∴∠1+∠4=180°-45°-90°=45°,
∴∠2=∠4,
即∠BAE=∠FEC;
(2)由(1)知∠BGE=45°,
∴∠AGE=135°,
∵CF是∠DCH的角平分线,
∴∠FCH=
| 1 |
| 2 |
∴∠ECF=135°,
∵四边形ABCD是正方形,
∴AB=BC,
∵G、E是AB、BC中点,
∴AG=
| 1 |
| 2 |
| 1 |
| 2 |
∴AG=EC,
在△AGE和△ECF中,
|
∴△AGE≌△ECF,
∴AE=EF,
在Rt△ABE中,∵AE2=AB2+BE2,
∴AE2=
| 5 |
| 4 |
∴S△AEF=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 5 |
| 4 |
| 5 |
| 8 |
点评:本题考查了正方形的性质、全等三角形的判定和性质、勾股定理、三角形外角性质,解题的关键是证明∠BAE=∠FEC,以及证明△AGE≌△ECF.

练习册系列答案
 长江作业本同步练习册系列答案
长江作业本同步练习册系列答案
相关题目