题目内容
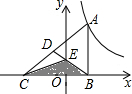 如图,等腰Rt△ABC的直角边BC在x轴上,斜边AC上的中线BD交y轴于点E,双曲线y=
如图,等腰Rt△ABC的直角边BC在x轴上,斜边AC上的中线BD交y轴于点E,双曲线y=| k |
| x |
| 2 |
分析:先根据题意证明△BOE∽△CBA,根据相似比及面积公式得出BO×AB的值即为|k|的值,再由函数所在的象限确定k的值.
解答:解:∵BD为Rt△ABC的斜边AC上的中线,
∴BD=DC,∠DBC=∠ACB,
又∠DBC=∠EBO,∴∠EBO=∠ACB,
 又∠BOE=∠CBA=90°,
又∠BOE=∠CBA=90°,
∴△BOE∽△CBA,
∴
=
,即BC×OE=BO×AB.
又∵S△BEC=4
,
∴
BC•EO=4
,
即BC×OE=8
=BO×AB=|k|.
又由于反比例函数图象在第一象限,k>0.
所以k等于8
.
故选B.
∴BD=DC,∠DBC=∠ACB,
又∠DBC=∠EBO,∴∠EBO=∠ACB,
 又∠BOE=∠CBA=90°,
又∠BOE=∠CBA=90°,∴△BOE∽△CBA,
∴
| BO |
| BC |
| OE |
| AB |
又∵S△BEC=4
| 2 |
∴
| 1 |
| 2 |
| 2 |
即BC×OE=8
| 2 |
又由于反比例函数图象在第一象限,k>0.
所以k等于8
| 2 |
故选B.
点评:此题主要考查了反比例函数y=
中k的几何意义,即过双曲线上任意一点引x轴、y轴垂线,所得矩形面积为|k|,是经常考查的一个知识点;这里体现了数形结合的思想,做此类题一定要正确理解k的几何意义.图象上的点与原点所连的线段、坐标轴、向坐标轴作垂线所围成的直角三角形面积S的关系即S=
|k|.
| k |
| x |
| 1 |
| 2 |

练习册系列答案
相关题目
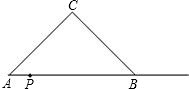 PQ=AP,以PQ为一边向上作正方形PQMN,设正方形PQMN与Rt△ABC重叠部分的面积为S.
PQ=AP,以PQ为一边向上作正方形PQMN,设正方形PQMN与Rt△ABC重叠部分的面积为S.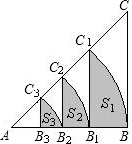 如图,等腰Rt△ABC的直角边长为4,以A为圆心,直角边AB为半径作弧BC1,交斜边AC于点C1,C1B1⊥AB于点B1,设弧BC1,C1B1,B1B围成的阴影部分的面积为S1,然后以A为圆心,AB1为半径作弧B1C2,交斜边AC于点C2,C2B2⊥AB于点B2,设弧B1C2,C2B2,B2B1围成的阴影部分的面积为S2,按此规律继续作下去,得到的阴影部分的面积S3=
如图,等腰Rt△ABC的直角边长为4,以A为圆心,直角边AB为半径作弧BC1,交斜边AC于点C1,C1B1⊥AB于点B1,设弧BC1,C1B1,B1B围成的阴影部分的面积为S1,然后以A为圆心,AB1为半径作弧B1C2,交斜边AC于点C2,C2B2⊥AB于点B2,设弧B1C2,C2B2,B2B1围成的阴影部分的面积为S2,按此规律继续作下去,得到的阴影部分的面积S3= 如图,等腰Rt△ABC中斜边AB=4,O是AB的中点,以O为圆心的半圆分别与两腰相切于点D、E,图中阴影部分的面积是多少?请你把它求出来.(结果用π表示)
如图,等腰Rt△ABC中斜边AB=4,O是AB的中点,以O为圆心的半圆分别与两腰相切于点D、E,图中阴影部分的面积是多少?请你把它求出来.(结果用π表示)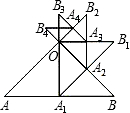 已知:如图,等腰Rt△OAB的直角边OA的长为1,以AB边上的高OA1为直角边,按逆时针方向作等腰Rt△OA1B1,A1B1与OB相交于点A2.若再以OA2为直角边按逆时针方向作等腰Rt△OA2B2,A2B2与OB1相交于点A3,按此作法进行下去,得到△OA3B3,△OA4B4,…,则△OA6B6的周长是
已知:如图,等腰Rt△OAB的直角边OA的长为1,以AB边上的高OA1为直角边,按逆时针方向作等腰Rt△OA1B1,A1B1与OB相交于点A2.若再以OA2为直角边按逆时针方向作等腰Rt△OA2B2,A2B2与OB1相交于点A3,按此作法进行下去,得到△OA3B3,△OA4B4,…,则△OA6B6的周长是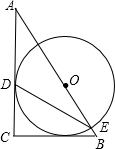 如图,等腰Rt△ABC,AC=BC,以斜边AB中点O为圆心作⊙O与AC边相切于点D,交AB于点E,连接DE.
如图,等腰Rt△ABC,AC=BC,以斜边AB中点O为圆心作⊙O与AC边相切于点D,交AB于点E,连接DE.