题目内容
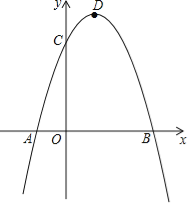
【题目】如果一条抛物线![]() 与x轴的两个交点为A,B(点A在点B的左侧,顶点为P,连接PA,PB,那么称
与x轴的两个交点为A,B(点A在点B的左侧,顶点为P,连接PA,PB,那么称![]() PAB为这条抛物线的“抛物线三角形”。
PAB为这条抛物线的“抛物线三角形”。
(1)请写出“抛物线三角形”是等腰直角三角形时,抛物线的表达式(写出一个即可);
(2)若抛物线![]() 的“抛物线三角形”是等边三角形,求b的值;
的“抛物线三角形”是等边三角形,求b的值;
(3)若抛物线![]() 不存在“抛物线三角形”则a,b,c之间应满足怎样的关系式?请直接写出关系式。
不存在“抛物线三角形”则a,b,c之间应满足怎样的关系式?请直接写出关系式。
【答案】(1)“抛物线三角形”是等腰直角三角形时,抛物线的表达式可以为![]() (答案不唯一);(2)
(答案不唯一);(2)![]() ;(3)
;(3)![]() .
.
【解析】
(1)利用等腰直角三角形的性质可知P点的纵坐标为AB的一半,据此可设出P、A、B的坐标,可写出抛物线的表达式;
(2)过点P作PH⊥AB于H,由等边三角形的性质可得到PH=![]() AH,再用b表示出P点坐标,则可得到关于b的方程,可求得b的值;
AH,再用b表示出P点坐标,则可得到关于b的方程,可求得b的值;
(3)由条件可知P、A、B三点不能构成三角形,则可知A、B重合或没有A、B两点,即抛物线与x轴有一个或没有交点,则可得到a、b、c的关系.
(1)不妨设抛物线的对称轴为![]() 轴,即设抛物线解析式为
轴,即设抛物线解析式为![]() ,
,
则![]() ,
,![]() ,
,![]() ,
,
∵![]() 为等腰直角三角形,
为等腰直角三角形,
∴![]() ,即
,即![]() ,解得
,解得![]() .
.
∴“抛物线三角形”是等腰直角三角形时,抛物线的表达式可以为![]() ;
;
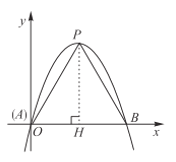
(2)如图,过点![]() 作
作![]() 于
于![]() ,
,
∵![]() 是等边三角形,
是等边三角形,
∴![]() ,
,
∵抛物线![]() 的顶点坐标为
的顶点坐标为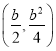 ,
,
∴![]() ,解得
,解得![]() ;
;
(3)当抛物线![]() 不存在“抛物线三角形”,
不存在“抛物线三角形”,
则![]() ,
,![]() ,
,![]() 三点不能构成三角形,即抛物线与
三点不能构成三角形,即抛物线与![]() 轴有一个或没有交点,
轴有一个或没有交点,
∴方程![]() 有两个相等的实数根或没有实数根,
有两个相等的实数根或没有实数根,
∴![]() .
.

 备战中考寒假系列答案
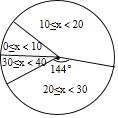
备战中考寒假系列答案【题目】体育组为了了解九年级450名学生排球垫球的情况,随机抽查了九年级部分学生进行排球垫球测试(单位:个),根据测试结果,制成了下面不完整的统计图表:
组别 | 个数段 | 频数 | 频率 |
1 |
| 5 | 0.1 |
2 |
| 21 | 0.42 |
3 |
|
| |
4 |
|
|
(1)表中的数![]() ,
,![]() ;
;
(2)估算该九年级排球垫球测试结果小于10的人数;
(3)排球垫球测试结果小于10的为不达标,若不达标的5人中有3个男生,2个女生,现从这5人中随机选出2人调查,试通过画树状图或列表的方法求选出的2人为一个男生一个女生的概率.