题目内容
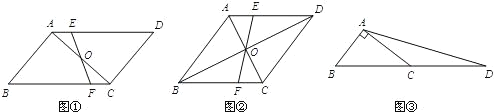
【题目】(1)猜想:如图①,在![]() 中,点
中,点![]() 是对角线
是对角线![]() 的中点,过点
的中点,过点![]() 的直线分别交
的直线分别交![]() 、
、![]() 于点
于点![]() 、
、![]() ,若
,若![]() 的面积是8,则四边形
的面积是8,则四边形![]() 的面积是________.
的面积是________.
(2)探究:如图②,在菱形![]() 中,对角线
中,对角线![]() 、
、![]() 交于点
交于点![]() ,过点
,过点![]() 的直线分别交
的直线分别交![]() 、
、![]() 于点
于点![]() 、
、![]() ,若
,若![]() ,
,![]() ,求四边形
,求四边形![]() 的面积.
的面积.
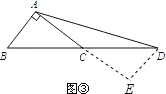
(3)应用:如图③,在![]() 中,
中,![]() ,延长
,延长![]() 到点
到点![]() ,使
,使![]() ,连结
,连结![]() ,若
,若![]() ,
,![]() ,则
,则![]() 的面积是_______.
的面积是_______.
【答案】(1)4;(2)12;(3)1.
【解析】
(1)首先根据平行四边形的性质可得AD∥BC,OA=OC.根据平行线的性质可得∠EAO=∠FCO,∠AEO=∠CFO,进而可根据AAS证明△AEO≌△CFO,再根据全等三角形的性质可得结论;
(2)根据菱形的性质得到AD∥BC,AO=CO,![]() ,根据全等三角形的判定定理得到△AOE≌△COF,于是得到结果;
,根据全等三角形的判定定理得到△AOE≌△COF,于是得到结果;
(3)延长AC到E使CE=AC=4,根据全等三角形的判定定理得到△ABC≌△CDE,由全等三角形的性质得到∠E=∠BAC=90°,根据勾股定理得到DE=3,即可得到结论.
(1) ∵四边形ABCD是平行四边形,
∴AD∥BC,OA=OC.
∴∠EAO=∠FCO,∠AEO=∠CFO,
在△AOE和△COF中,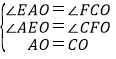 ,
,
∴△AEO≌△CFO(AAS),
∴四边形CDEF的面积=S△ACD=![]() ABCD的面积=4;
ABCD的面积=4;
故答案为:4;;
(2)∵四边形![]() 是菱形
是菱形
∴![]() ,
,![]() ,
,![]() ,
,
∴![]()
在![]() 和
和![]() 中,
中,
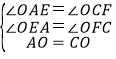
∴![]() .
.
∴四边形![]() 的面积
的面积![]() 的面积
的面积
![]()
由勾股定理可求得![]()
∴![]()
∴四边形![]() 的面积
的面积![]() 的面积
的面积![]() ;
;
(3) 延长AC到E使CE=AC=1,
在△ABC与△CDE中,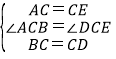 ,
,
∴△ABC≌△CDE(SAS),
∴∠E=∠BAC=90°,
∴DE=![]() ,
,
∴S△ABD=S△ADE=![]() AEDE=
AEDE=![]() ×2×1=1.
×2×1=1.
故答案为:1.

【题目】我区某陶瓷厂计划一周生产陶瓷工艺品350个,平均每天生产50个,但实际每天生产量与计划相比有出入,下表是某周的生产情况(以50个为标准,超产记为正、减产记为负):
星期 | 一 | 二 | 三 | 四 | 五 | 六 | 日 |
增减(单位:个) | +4 | -6 | -7 | +15 | -5 | +16 | -8 |
(1)根据记录的数据,请直接写出该厂本周产量最多的一天比最少的一天多生产的工艺品的个数;
(2)该工艺厂在本周实际生产工艺品的数量为多少个?(列式计算);
(3)已知该厂实行每周计件工资制,每周结算一次,每生产一个工艺品可得6元,若超额完成任务(以350个为标准),则超过部分每个另奖12元,少生产每个扣4元,试求该陶瓷厂在这一周应付出的工资总额.
【题目】三峡水库在正常运用情况下,为满足兴利除害的要求而蓄到的最高蓄水位为![]() 米,每年汛期允许蓄水的最大水位为
米,每年汛期允许蓄水的最大水位为![]() 米。在每年汛期,保证上游水位在
米。在每年汛期,保证上游水位在![]() 米的防洪限制水位,多出
米的防洪限制水位,多出![]() 米的相应库容以迎接洪峰。洪峰后,超过
米的相应库容以迎接洪峰。洪峰后,超过![]() 米的水量下泄,为下次洪峰做准备,下泄的水使中下游江面的水位升高,但不影响人们的生命和财产安全。监测水位变化的数据为防洪抗旱提供重要依据,根据多年统计,洪峰到达时万州监测点的平均水位为
米的水量下泄,为下次洪峰做准备,下泄的水使中下游江面的水位升高,但不影响人们的生命和财产安全。监测水位变化的数据为防洪抗旱提供重要依据,根据多年统计,洪峰到达时万州监测点的平均水位为![]() 米。下列是水位监测员小刘在汛期某一周每天同一时间统计的长江(万州监测点)水位高低的变化情况:(单位:米,用正数记水位比
米。下列是水位监测员小刘在汛期某一周每天同一时间统计的长江(万州监测点)水位高低的变化情况:(单位:米,用正数记水位比![]() 米的上升数,用负数记下降数)
米的上升数,用负数记下降数)
星期 | 一 | 二 | 三 | 四 | 五 | 六 | 日 |
水位变化 |
|
|
|
|
|
|
|
(1)本周星期三万州监测点的实际水位是多少?
(2)若水位每上升![]() 米,蓄水量将增加
米,蓄水量将增加![]() 亿立方米,则根据数据显示,星期六的蓄水量比星期四的蓄水量增加了多少亿立方米?
亿立方米,则根据数据显示,星期六的蓄水量比星期四的蓄水量增加了多少亿立方米?