题目内容
【题目】已知：如图，AD∥BC，ED∥BF，且AF=CE． 求证：四边形ABCD是平行四边形．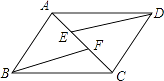
【答案】证明：∵AD∥BC，ED∥BF，且AF=CE， ∴∠DAC=∠ACB，∠DEF=∠EFB，AE=FC，
∴∠AED=∠BFC，
∴△AED≌△BCF，
∴AD=BC，
∴四边形ABCD是平行四边形．
【解析】由已知条件可得AE=FC，∠DAC=∠ACB，∠DEF=∠EFB，AE=FC，证得△AED≌△BCF，从而证得．
【考点精析】认真审题，首先需要了解平行四边形的判定(两组对边分别平行的四边形是平行四边形：两组对边分别相等的四边形是平行四边形；一组对边平行且相等的四边形是平行四边形；两组对角分别相等的四边形是平行四边形；对角线互相平分的四边形是平行四边形)．
练习册系列答案
新辅教导学系列答案
阳光同学一线名师全优好卷系列答案
相关题目
