题目内容
 如图,在直角三角形ABC中,∠C=90°,AB=4,阴影部分的面积为
如图,在直角三角形ABC中,∠C=90°,AB=4,阴影部分的面积为
- A.2π
- B.3π
- C.4π
- D.6π
C
分析:根据勾股定理以及圆面积公式,可以发现并证明:以直角三角形的两条直角边为直径的半圆面积等于以斜边为直径的半圆面积.所以阴影部分的面积是以斜边为直径的圆面积即4π.
解答:阴影部分的面积= π(
π(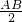 )2+
)2+ π(
π( )2+
)2+ π(
π(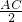 )2=
)2= π(AB2+BC2+AC2)
π(AB2+BC2+AC2)
∵AB2=BC2+AC2
∴阴影部分的面积= π×2AB2=
π×2AB2= π•AB2=4π.故选C.
π•AB2=4π.故选C.
点评:熟练运用勾股定理证明:以直角三角形的两条直角边为直径的半圆面积等于以斜边为直径的半圆面积.此结论在计算的过程中运用可以简便计算.
分析:根据勾股定理以及圆面积公式,可以发现并证明:以直角三角形的两条直角边为直径的半圆面积等于以斜边为直径的半圆面积.所以阴影部分的面积是以斜边为直径的圆面积即4π.
解答:阴影部分的面积=
 π(
π(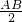 )2+
)2+ π(
π( )2+
)2+ π(
π(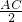 )2=
)2= π(AB2+BC2+AC2)
π(AB2+BC2+AC2)∵AB2=BC2+AC2
∴阴影部分的面积=
 π×2AB2=
π×2AB2= π•AB2=4π.故选C.
π•AB2=4π.故选C.点评:熟练运用勾股定理证明:以直角三角形的两条直角边为直径的半圆面积等于以斜边为直径的半圆面积.此结论在计算的过程中运用可以简便计算.

练习册系列答案
相关题目
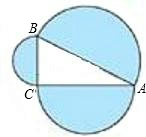 如图,在直角三角形ABC中,∠C=90°,AB=4,阴影部分的面积为( )
如图,在直角三角形ABC中,∠C=90°,AB=4,阴影部分的面积为( )| A、2π | B、3π | C、4π | D、6π |
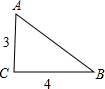
 如图,在直角三角形中,一直角边比另一直角边长1,且斜边长为5.
如图,在直角三角形中,一直角边比另一直角边长1,且斜边长为5.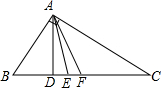 如图,在直角三角形ABC中,AD为斜边上的垂线,AE为角平分线,AF为中线,
如图,在直角三角形ABC中,AD为斜边上的垂线,AE为角平分线,AF为中线,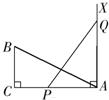 9、如图,在直角三角形ABC中,∠C=90°,AC=10cm,BC=5cm,一条线段PQ=AB,P、Q两点分别在AC和AC的垂线AX上移动,则当AP=
9、如图,在直角三角形ABC中,∠C=90°,AC=10cm,BC=5cm,一条线段PQ=AB,P、Q两点分别在AC和AC的垂线AX上移动,则当AP=