Question

【题目】如图，四边形ABCD是正方形，E是CD上的一点，△ABF是△ADE的旋转图形．
（1）写成由△ADE顺时针旋转到△ABF的旋转中心、旋转角的度数．
（2）连接EF，判断并说明△AEF的形状．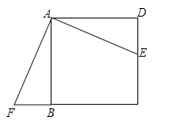

Answer 1

【答案】解：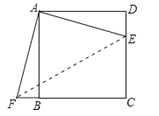

（1)∵△ABF是△ADE的旋转图形，
∴旋转中心是点A；
∵顺时针旋转了90，
∴旋转角的度数90；
（2）△AEF的形状是等腰直角三角形，理由如下：
∵△ABF是△ADE的旋转图形，旋转角为90°，
∴AE=AF，∠FAE=90°，
∴△AEF是等腰直角三角形．
【解析】（1）利用旋转的性质得出旋转中心即可；利用旋转的位置得出旋转角即可；
（2）利用旋转的性质以及等腰三角形的判定得出即可．
【考点精析】根据题目的已知条件，利用旋转的性质的相关知识可以得到问题的答案，需要掌握①旋转后对应的线段长短不变，旋转角度大小不变；②旋转后对应的点到旋转到旋转中心的距离不变；③旋转后物体或图形不变，只是位置变了．