题目内容
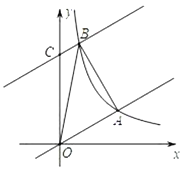
【题目】如图,在平面直角坐标系中,直线![]() ,与反比例函数
,与反比例函数![]() 在第一象限内的图象相交于点
在第一象限内的图象相交于点![]()
(1)求该反比例函数的表达式;
(2)将直线![]() 沿
沿![]() 轴向上平移
轴向上平移![]() 个单位后与反比例函数在第一象限内的图象相交于点
个单位后与反比例函数在第一象限内的图象相交于点![]() ,与
,与![]() 轴交于点
轴交于点![]() ,若
,若![]() ,连接
,连接![]() ,
,![]() .
.
①求![]() 的值;
的值;
②判断![]() 与
与![]() 的位置关系,并说明理由;
的位置关系,并说明理由;
(3)在(2)的条件下,在射线![]() 上有一点
上有一点![]() (不与
(不与![]() 重合),使
重合),使![]() ,求点
,求点![]() 的坐标.
的坐标.
【答案】(1)![]() ;(2)①
;(2)①![]() ;②
;②![]() ;(3)
;(3)![]() .
.
【解析】
(1)先确定出点A坐标,再用待定系数法求出反比例函数解析式;
(2)①先求出点B坐标即可得出结论;②利用勾股定理的逆定理即可判断;
(3)利用相似三角形的性质得出AP,进而求出OP,再求出∠AOH=30°,最后用含30°的直角三角形的性质即可得出结论.
解:(1)∵点![]() 在直线
在直线![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴点![]() ,
,
∵点![]() 在反比例函数
在反比例函数![]() 上,
上,
∴![]() ,
,
∴![]() ;
;
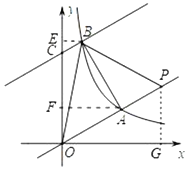
(2)①作![]() 轴于
轴于![]() ,
,![]() 轴于
轴于![]() .
.
∴![]() ,
,
∵![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴设![]() 的解析式为
的解析式为![]() ,
,
∵经过点![]() ,
,
∴![]() .
.
∴直线![]() 的解析式为
的解析式为![]() ,
,
∴![]() .
.
②∵![]() ,
,![]() ,
,
∴![]() ,
,![]() ,
,![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() .
.
(3)如图
∵![]() ,
,![]() ,
,
由(2)知,![]() ,
,![]()
即![]() ,
,
∴![]() ,
,
∵![]() ,
,
∴![]() ,
,
过点![]() 作
作![]() 轴于
轴于![]()
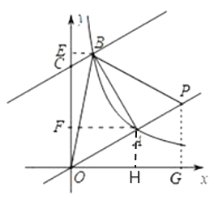
∵![]() ,
,
∴![]() ,
,![]() ,
,
在![]() 中,
中,
∴![]() ,
,
∴![]()
过点![]() 作
作![]() 轴于
轴于![]() ,
,
在![]() 中,
中,![]() ,
,![]() ,
,
∴![]() ,
,![]() ,
,
∴![]() .
.

【题目】射击训练班中的甲、乙两名选手在5次射击训练中的成绩依次为(单位:环):
甲:8,8,7,8,9
乙:5,9,7,10,9
教练根据他们的成绩绘制了如下尚不完整的统计图表:
选手 | 平均数 | 众数 | 中位数 | 方差 |
甲 | 8 | b | 8 | 0.4 |
乙 | α | 9 | c | 3.2 |
根据以上信息,请解答下面的问题:
(1)α= ,b= ,c= ;
(2)完成图中表示乙成绩变化情况的折线;
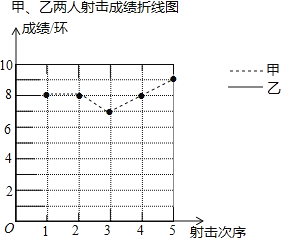
(3)教练根据这5次成绩,决定选择甲参加射击比赛,教练的理由是什么?
(4)若选手乙再射击第6次,命中的成绩是8环,则选手乙这6次射击成绩的方差与前5次射击成绩的方差相比会 .(填“变大”、“变小”或“不变”)