题目内容
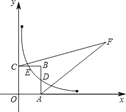
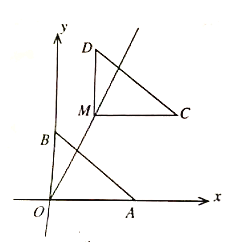
【题目】如图,点![]() 在直线
在直线![]() 上,点
上,点![]() 的坐标分别是
的坐标分别是![]() ,连接
,连接![]() ,将
,将![]() 沿射线
沿射线![]() 方向平移,使点O移动到点M,得到
方向平移,使点O移动到点M,得到![]() (点
(点![]() 分别对应点
分别对应点![]() ).
).
(1)填空:m的值为_____________,点C的坐标是______________;
(2)在射线![]() 上是否存在一点N,使
上是否存在一点N,使![]() ,如果存在,请求出点N的坐标;如果不存在,请说明理由;
,如果存在,请求出点N的坐标;如果不存在,请说明理由;
(3)连接![]() ,点P是射线
,点P是射线![]() 上一动点,请直接写出使
上一动点,请直接写出使![]() 是等腰三角形时点P的坐标.
是等腰三角形时点P的坐标.
【答案】(1)![]() ;(2)
;(2)![]() 或
或![]() ;(3)(
;(3)(![]() ,
,![]() )或(
)或(![]() ,
,![]() ) 或(0,0)或(
) 或(0,0)或(![]() ,
,![]() ) 或(
) 或(![]() ,
,![]() ).
).
【解析】
(1)当x=2时,y=2x=4,故:m=4,则点M的坐标为(2,4),由平移,可知:CM=AO=4,即可求解;
(2)存在,理由:分当NC在直线MC下方、上方,两种情况分别求解即可;
(3)分AD=AP、AD=PD、AP=PD三种情况,分别求解即可.
解:(1)当x=2时,y=2x=4,
∴m=4,∴点M的坐标为(2,4),
由平移,可知:CM=AO=4,
∴点C的坐标为(6,4),则点D(2,6).
故答案为:4;(6,4).
(2)存在,理由:
①当NC在直线MC下方时,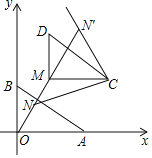
直线OM的表达式为:y=2x…①,
则tan∠MOB=![]() ,
,
∠NCM=∠BOM,则tan∠NCM=![]() ,
,
设直线NC的表达式为:y=![]()
将点C的坐标代入上式并解得:b=1,
则直线NC的表达式为:y=![]()
将①②联立并求解得:x=![]() ,
,
则点N(![]() ,
,![]() ) ;
) ;
②当NC在直线MC上方时,
同理可得:点N′(![]() ,
,![]() );
);
故点N(![]() ,
,![]() ) 或(
) 或(![]() ,
,![]() );
);
(3)设点P(x,2x),点D(2,6),点A(4,0),
则AD2=4+36=40,AP2=(x-4)2+4x2=5x2-8x+16,PD2=(x-2)2+(2x-6)2=5x2-28x+40,
①当AD=AP时,40=5x2-8x+16,解得:x=![]() ,
,
②当AD=PD时,同理可得:x=0或![]() ,
,
③当AP=PD时,同理可得:x=![]() ,
,
故点P坐标为(![]() ,
,![]() )或(
)或(![]() ,
,![]() ) 或(0,0)或(
) 或(0,0)或(![]() ,
,![]() ) 或(
) 或(![]() ,
,![]() ).
).