Question

如图，AB是半圆O的直径，C为半圆上一点，E是BC的中点，AE交BC于点D，DF⊥AB于F，F为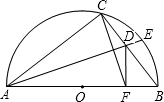垂足，连接CF．
（1）判断△CDF的形状，并证明你的结论；
（2）若AC=8，cos∠CAB=

4

5

，求线段BC和CD的长．

Answer 1

分析：（1）易得∠CAE=∠BAE，∠ACB=∠DFC=90°，再加上公共边，可证得△CDA≌△FDA，即证CD=DF．
（2）利用cos∠CAB的值可求得BC长，设出CD=DF=x，根据勾股定理列出关于x的方程，求出方程的解即可得到CD的长．

解答：解：（1）等腰三角形．
∵E是BC的中点，
∴∠CAE=∠BAE．
∵AB是半圆O的直径，DF⊥AB于F，
∴∠ACB=∠DFA=90．
又∵AD=AD，
∴△CDA≌△FDA．
∴CD=DF．

（2）∵AC=8，cos∠CAB=

4

5

，
∴BC=6．
根据勾股定理得：AB=10，
∵△CDA≌△FDA．
∴AC=AF=8，
∴FB=2，
设CD=DF=x，则BD=BC-CD=6-x，
根据勾股定理得：x²+2²=（6-x）²，
解得：x=

8

3

∴CD=

8

3

．

点评：本题考查了同弧所对的圆周角相等，直角三角形的三角函数，以及角平分线所截得的线段的对于比等知识点．